Рекурсивная деконволюция

...........................................

...........................................

a_N h₀^-1 + a_N-1 h₁^-1 + a_N-2 h₂^-1 + a_N-3 h₃^-1 +... +a₀ h_N^-1 = 0

Пример расчета оптимального фильтра деконволюции.

Повторим инверсию оператора, приведенного на рис. 13.2.1, N=6.

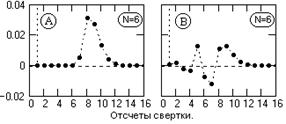Рис. 13.3.1.

Значения оптимального инверсного оператора в сопоставлении с усеченным:

h^-1(n) = {4.56, -6.033, 2.632, 0.417, -0.698, -0.062, 0.267} – прямой расчет по (13.2.2).

h^-1(n) = {4.557, -6.026, 2.633, 0.397, -0.693, -0.009, 0.145} – расчет по (13.3.5).

Значения свертки инверсных операторов с прямыми и метрики приближения:

Оператор по (13.2.2) – рис. 13.3.1(А): s_n= {1, 0, 0, 0, 0, 0, 0, 0.005, 0.031, 0.027, 0.013, 0.004, 0.001, 0, 0,…}. E=0.044.

Оператор по (13.3.5) – рис. 13.3.1(В): s_n= {0.999, <0.001, 0.002, -0.003, -0.003, 0.013, -0.008, -0.012, 0.011, 0.013, 0.007, 0.002, <0.001, 0, 0, …}. E=0.027.

Метрика приближения оптимального оператора в 1.6 раза меньше усеченного.

Как видно на рис. 13.3.1, оптимизация инверсного оператора заключается в центрировании ошибок приближения и с распределением по интервалу суммарной длины прямого и инверсного оператора.

Уравнение оптимальной инверсии. Оптимальный инверсный фильтр может быть получен непосредственно с использованием z-образов импульсной реакции и автоковариационной функции прямого фильтра. Если для прямого фильтра мы имеем передаточную функцию H(z), то z-образ автоковариационной функции фильтра (как z-отображение спектральной плотности мощности) представляет собой произведение:

A(z) = H(z)H*(z), (13.3.6)

где H*(z)- функция, комплексно сопряженная с H(z). Переносим H(z) в левую часть формулы и для функций диракоидного типа заменяем выражение 1/H(z) = H^-1(z):

А(z)H^-1(z) = H*(z). (13.3.7)

Запишем последнее равенство в развернутом виде:

(a_-Nz^-N+... +a_-1z^-1+a₀+a₁z¹+... +a_Nz^N)(h₀^-1+h₁^-1z¹+h₂^-1z²+... +h_N^-1z^N) =

= h₀*+h₁*z^-1+h₂*z^-2+... +h_N*z^N. (13.3.8)

В выражении (13.3.8) сумма коэффициентов при одинаковых степенях z в левой части равенства должна быть равна коэффициенту при соответствующей степени z в правой части равенства, что позволяет составить следующую систему из N уравнений для коэффициентов при степенях z⁰, z¹, z²,..., z^N:

a₀ h₀^-1 + a_-1 h₁^-1 + a_-2 h₂^-1 + a_-3 h₃^-1 +... + a_-N h_N^-1 = h₀* (13.3.9)

a₁ h₀^-1 + a₀ h₁^-1 + a_-1 h₂^-1 + a_-2 h₃^-1 +... + a_-N-1 h_N^-1 = 0

a₂ h₀^-1 + a₁ h₁^-1 + a₀ h₂^-1 + a₅ h₃^-1 +... + a_-N-2 h_N^-1 = 0

a_N h₀^-1 + a_N-1 h₁^-1 + a_N-2 h₂^-1 + a_N-3 h₃^-1 +... +a₀ h_-N ^-1 = 0

В случае вещественных фильтров, когда a_i = a_-i и h₀* = h₀, уравнение (13.3.9) идентично уравнению (13.3.5).

Уравнение Левинсона. Практический способ расчета оптимальных инверсных фильтров по уравнению (13.3.9) предложен в 1947 году Н.Левинсоном.

Перепишем уравнение (13.3.9) в матричной форме:

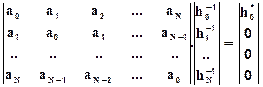(13.3.10)

Так как коэффициенты инверсного фильтра достаточно определить с точностью до произвольного масштабного множителя, приведем h_o^-1 к 1, a функцию автоковариации переведем в функцию коэффициентов корреляции делением обеих частей уравнения на а_о. Обозначая A_i = a_i/a_o, W_i = h_i^-1/h_o^-1 и V = h_o*/(h_o^-1a_o) = h_oh_o*/a_o, получаем:

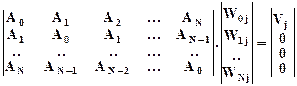(13.3.11)

где для значений W и V введен индекс j номеров предстоящих итераций по циклу вычисления коэффициентов фильтра.

При нулевой итерации (N=0, j=0) имеем только одно уравнение:

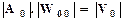. (13.3.12)

Благодаря проведенной нормировке решения уравнения (13.3.12) не требуется:

А₀= 1, V₀= 1, W₀₀= 1.

Составим уравнение для двучленного фильтра (N=1, j=1):

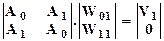(13.3.13)

Перепишем уравнение (13.3.12) в прямой форме:

А₀ W₀₀ = V₀. (13.3.14)

Запишем вспомогательную систему, для чего к уравнению (13.3.14) добавим вторую строку с новой постоянной E_j:

A₀ W₀₀ + A₁·0 = V_0,

A₁ W₀₀ + A₀ ·0 = E₁.

В матричной форме:

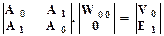(13.3.15)

Реверсируем уравнение (13.3.15):

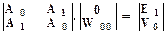(13.3.16)

Вычтем (13.3.16) из (13.3.15) с неопределенным множителем R_j:

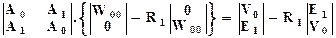(13.3.17)

Из верхней строки уравнения (13.3.16) можно получить значение Е₁:

Е₁= A₁W₀₀. (13.3.18)

Уравнение (13.3.13) можно сделать равнозначным уравнению (13.3.17), если правую часть нижней строки уравнения (13.3.17) приравнять к правой части нижней строки уравнения (13.3.13):

E₁ - R₁V₀ = 0, R₁ = E₁/V₀. (13.3.19)

При этом из правых частей верхних строк уравнений (13.3.13, 13.3.17) будем иметь:

V₁ = V₀ - R₁E₁. (13.3.20)

Приравнивая друг другу левые части уравнений (13.3.13,13.3.17), получаем:

W₀₁ = W₀₀ - R₁·0 = W₀₀ = 1.

W₁₁ = 0 - R₁W₀₀ = -R₁W₀₀. (13.3.21)

Этим заканчивается первая итерация. Аналогично, для второй итерации:

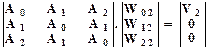(13.3.22)

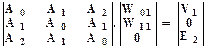(13.3.23)

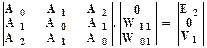(13.3.24)

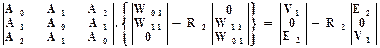(13.3.25)

Из верхней строки уравнения (13.3.24):

Е₂ = A₁W₁₁+A₂W₀₁.

Из правых частей нижней и верхней строк уравнений (13.3.22, 13.3.25):

R₂ = E₂/V₁,

V₂ = V₁ - R₂E₂.

Новые коэффициенты из левых частей уравнений (13.3.22, 13.3.25):

W₀₂ = W₀₁ - R₂ 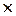0= 1,

W₁₂ = W₁₁ - R₂W₁₁,

W₂₂ = 0 - R₂W₀₁.

Анализ расчетов позволяет вывести следующие рекуррентные формулы:

E_j =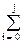A_iW_j-i,_j , j = 1,2,...,M. (13.3.26)

R_j = E_j/V_j-1,

V_j = V_j-1 - R_jE_j,

W_i,j = W_i,j-1 - R_jW_j-1,_j-1, i = 0,1,.., j.

Подпрограммы решения уравнений для ЭВМ приведены в литературе.

Уравнение фильтра рекурсивной деконволюции. Запишем уравнение (13.1.2) для инверсного фильтра в развернутой форме:

H^-1(z) = 1/(h₀+h₁z+h₂z²+...). (13.4.1)

Так как для минимально-фазового оператора всегда выполняется условие h₀ 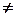0, приведем (13.4.1) к виду:

H^-1(z) = (1/h₀)/(1+h₁z/h₀+h₂z²/h₀+...) = G/(1+q₁z+q₂z²+...), (13.4.2)

где: G = 1/h₀, q₁ = h₁/h₀, q₂ = h₂/h₀ и т.д. Но уравнение (13.4.2) есть не что иное, как уравнение передаточной функции рекурсивного фильтра, где цепь обратной связи образована коэффициентами нормированного оператора h(n). Алгоритм вычислений:

y_k = G·x_k –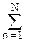q_n·y_k-n.

Выражение (13.4.2) уникально по своим возможностям. В принципе, оно может реализовать оператор инверсной фильтрации с бесконечным импульсным откликом. На практике оно может использоваться вместо медленно затухающих инверсных операторов, модуль одного из полюсов которого очень близок к 1 (менее 1.1) при высоких требованиях к метрике приближения.

Пример рекурсивной деконволюции.

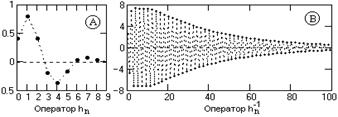Рис.13.4.1.

Оператор h_n = {0.41, 0.791, 0.401, -0.193, -0.367, -0.166, 0.032, 0.068, 0.027, -0.001}, N=9.

1. Модуль одного из корней фильтра равен 1.032, что приводит к очень слабому затуханию инверсного оператора. Метрика приближения даже при N=100 для усеченного оператора составляет 0.3. Форма операторов приведена на рис. 13.4.1.

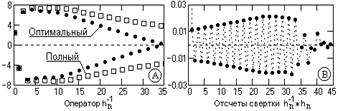Рис.13.4.2.

2. При использовании оптимального инверсного оператора с N=100 значение погрешности приближения уменьшается более чем в 20 раз, что позволяет уменьшить длину оператора до N=35 при погрешности приближения порядка 0.1 (рис 13.4.2(А)), при этом абсолютные значения погрешностей приближения не превышают 0.03 (рис. 13.4.2(В)).

3. Расчет коэффициентов фильтра рекурсивной деконволюции:

G = 1/h_o = 2.441

g_n = h_n·G. g_n = {1.932, 0.978, -0.472, -0.896, -0.405, 0.077, 0.165, 0.065, -0.003}, n=1, …, 9.

Рис. 13.4.3.

На рис. 13.4.3 приведен результат рекурсивной деконволюции оператора h_n. Деконволюция абсолютно точно, с нулевой метрикой, восстанавливает импульс Кронекера, хотя собственный импульсный отклик рекурсивного оператора повторяет оператор h^-1_n при его вычислении по формуле (13.2.2) и длительность его значимой части близка к 200. Коэффициент усиления дисперсии шумов при данной операции вычисляется по значениям импульсного отклика оператора рекурсивной деконволюции и весьма существенен, как и для всех инверсных операторов.

Дата добавления: 2014-01-03