
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критическая скорость
|
|
|
|
Влияние мелководья на скорость движения судна.
Сопротивление воды движению судна условно делят на вязкостное и волновое. Влияние мелководья на скорость движения судна заключается в изменении как вязкостного, так и волнового сопротивлений.
Увеличение вязкостного сопротивления на мелководье связано с изменением поля вызванных скоростей. В разделе 11.1 были вкратце описаны причины увеличения скорости потока воды, огибающей корпус судна при движении на мелководье и в канале. А рост скоростного потока, естественно, приводит к росту вязкостного сопротивления.
Рост вязкостного сопротивления сильно зависит от соотношения глубины и осадки судна, что наглядно отражено на графике (рис.111.8), полученном на основании материалов испытаний модели судна.
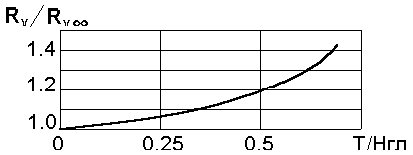
Рис.11.8 Рост сопротивления судна
Здесь величина Rv / Rv оо - есть отношение вязкостных сопротивлений на мелководье и на глубокой воде соответственно.
Еще большее изменение при ограничении глубины претерпевает волновое сопротивление. Как уже упоминалось выше, движущееся судно создает вокруг себя систему поперечных волн и систему расходящихся волн в виде сектора. Из теории волн относительно малой амплитуды известно, что при равных скоростях распространения прогрессивных волн их длина λ на мелкой воде больше, чем на глубокой.
Зависимость между длиной волны от ее скоростью определяется следующим выражением:

| (11.17) |
Предельной скоростью распространения волн данного типа в условиях мелководья является критическая скорость Vкр, соответствующая числу Фруда по глубине FrH ≈ 1, м/с:
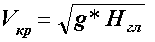
| (11.18) |
Из этого следует, что предельная длина волн данного типа на мелководье зависит от глубины:
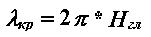
| (11.19) |
Однако, скорость волн, создаваемых движущимся судном, зависит от скорости судна. И поскольку существует зависимость между длиной волны и ее скоростью, то задавая скорость расходящимся волнам судно тем самым задает им и длину.
Исходя из выражения (11.19) получается, что если глубина моря ограничивает предельную длину волн, то этим она задает предельно возможную скорость распространения волн.
По мере приближения скорости судна Vc к критическому значению Vкр (либо увеличение скорости судна, либо уменьшение глубины моря) длины расходящихся волн увеличиваются, что приводит к расширению волнового сектора. Расширяющийся сектор взволнованной поверхности требует все больших энергетических затрат на свое поддержание. И наконец, при Vc ≈ Vкр, когда угол фронта расходящихся волн носовой и кормовой групп с диаметральной плоскостью судна близок к 90о, происходит сложение поперечных и расходящихся систем волн, образуются две мощные поперечные волны, которые как бы запирают судно.
Поскольку волны достигли предельной длины (и соответственно, предельной скорости) и двигаться быстрее уже не могут, то дальнейшее увеличение мощности, передаваемой на винт, приводит лишь к увеличению амплитуды этих волн, но не дает увеличения скорости судна. Для преодоления этого барьера двигатель должен развить такую мощность, которая бы на глубокой воде соответствовала скорости судна на 5-6 узлов больше, чем эта Vкр
Потерю скорости на мелководье (в %) при плавании в зоне докритических скоростей можно приближенно рассчитать по эмпирической формуле Демина [11.6]:
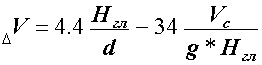
| (11.20) |
Значение должно получаться со знаком “минус”, если же получается положительное значение, то потерю скорости считают равной нулю.
После преодоления судном критической скорости поперечные волны им больше не создаются, и остаются лишь расходящиеся волны, что приводит к существенному уменьшению волнового сопротивления.
Мощная поперечная волна, образующаяся при достижении судном скорости, близкой к критической, не подчиняется теории волн относительно малой амплитуды, и скорость ее дальнейшего движения уже не зависит от скорости судна. Эта волна (“ спутная волна ”) может самостоятельно перемещаться на очень большие расстояния со скоростью, при которой она образовалась. Так академик А.Н.Крылов в книге “Мои воспоминания” описывает случай, когда спутной волной, образовавшейся в 6 милях от берега при прохождении над банкой миноносца “Новик” в 1912 году, был смыт с пристани 6-летний мальчик.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 724; Нарушение авторских прав?; Мы поможем в написании вашей работы!