
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Байеса, вероятность появления хотя бы одного события
|
|
|
|
Текст лекции
Лекция 4 Формула Байеса, вероятность появления хотя бы одного события
Учебные и воспитательные цели:
1. Изучить частную теорему о повторении опытов.
2. Изучить порядок определения вероятности события не менее заданного числа раз.
Вид занятия: лекция.
Продолжительность занятия: 90 минут.
Учебно-материальное обеспечение занятия:
Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).
Литература:
а) основная:
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. – 575 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. – М.: Высшая школа», 2004 г. – 480 с.
Структура занятия и расчёт времени
| Структура занятия | Время, мин |
| I. Вводная часть занятия | |
| II. Основная часть занятия | |
| 1. Формула Байеса, вероятность появления хотя бы одного события | |
| III. Заключительная часть занятия |
Пусть имеется полная группа несовместных гипотез 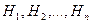 с известными вероятностями их наступления
с известными вероятностями их наступления 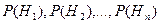 . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности 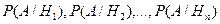 .
.
Требуется определить какие вероятности имеют гипотезы 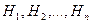 относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности 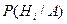 .
.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.
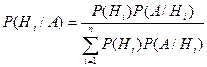 .
.
Эта формула называется формулой Байеса.
Доказательство.
По Теореме умножения вероятностей получаем:
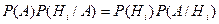 .
.
Тогда если 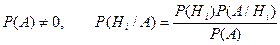 .
.
Для нахождения вероятности P (A) используем формулу полной вероятности.
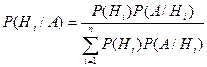 .
.
Если до испытания все гипотезы равновероятны с вероятностью 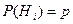 , то формула Байеса примет вид:
, то формула Байеса примет вид:

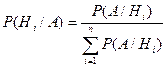 .
.
Пример. Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов – специалист средней квалификации. Вероятность того, что прибор, собранный специалистом высшей квалификации, надёжен, равна 0,9. Для специалиста средней квалификации эта вероятность равна 0,8. Взятый наудачу прибор оказался надёжным. Найти вероятность того, что этот прибор собран специалистом высшей квалификации.
Решение: пусть событие 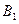 – появление прибора, собранного специалистом высшей квалификации; событие
– появление прибора, собранного специалистом высшей квалификации; событие 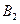 – появление прибора, собранного специалистом средней квалификации. Вероятности этих событий равны соответственно
– появление прибора, собранного специалистом средней квалификации. Вероятности этих событий равны соответственно 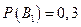 ,
, 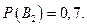
Пусть событие 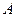 означает появление надёжного прибора. По условию примера вероятность события
означает появление надёжного прибора. По условию примера вероятность события 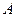 при условии, что появится прибор, собранный специалистом высшей квалификации,
при условии, что появится прибор, собранный специалистом высшей квалификации, 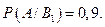 Аналогично вероятность появления надёжного прибора при условии, что появится прибор, собранный специалистом средней квалификации,
Аналогично вероятность появления надёжного прибора при условии, что появится прибор, собранный специалистом средней квалификации, 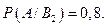 Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события
Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события 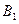 при условии, что появилось событие
при условии, что появилось событие 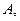 определяется по формуле
определяется по формуле
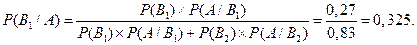
Заключительная часть занятия:
· напомнить тему и учебные вопросы занятия;
· отметить степень достижения учебных целей;
· ответить на возникшие вопросы у студентов;
На занятии иметь:
Калькуляторы – на каждого
Изучить:
1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. М.: Высшая школа, 2002 г. – 575 с., стр. 59-61.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. – М.: Высшая школа», 2004 г. – 480 с. стр. 55-61.
|
|
|
Дата добавления: 2014-01-03; Просмотров: 737; Нарушение авторских прав?; Мы поможем в написании вашей работы!