Графическое изображение вариационных рядов

Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная кривая.

Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами (х; т_х), где х — вариант, а т_х — соответствующая ему частота. Иногда вместо точек (х; т_х) строят точки (x; w_x). Затем эти точки соединяют последовательно отрезками. Крайние левую и правую точки соединяют соответственно с точками, изображающими ближайший снизу к наименьшему и ближайший сверху к наибольшему варианты. Пoлyчeнная ломаная линия называется полигоном.

Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.

Если по оси абсцисс выбрать такой масштаб, чтобы ширина интервала была равна единице, и считать, что по оси ординат единица масштаба соответствует одному наблюдению, то площадь гистограммы равна общему числу наблюдений, если по оси ординат откладывались частоты, и эта площадь равна единице, если откладывались частости.

Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.

Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами ( 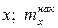), где х — вариант, 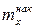— соответствующая накопленная частота. Иногда вместо точек (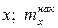) строят точки ( 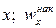). Полученные точки соединяют отрезками.

Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала — накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного.

Построение вариационного ряда — первый шаг к осмысливанию ряда наблюдений. Однако на практике этого недостаточно, особенно когда необходимо сравнить два ряда или более. Сравнению подлежат только так называемые однотипные вариационные ряды, т. е. ряды, которые построены по результатам обработки сходных статистических данных. Например, можно сравнивать распределения рабочих по возрасту на двух заводах или распределения времени простоев станков одного вида. Однотипные вариационные ряды обычно имеют похожую форму при графическом изображении, однако могут отличаться друг от друга, а именно: иметь различные значения признака, вокруг которых концентрируются наблюдения (меры этой качественной особенности называется средними величинами); различаться рассеянием наблюдений вокруг средних величин (меры этой особенности получили название показателей вариации).

Средние величины и показатели вариации позволяют судить о характерных особенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности.

Дата добавления: 2014-01-03