Лекция №1

Кіріспе. Проекциялау әдістері. Монж әдісі

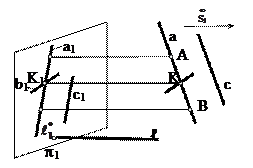
Кеңістіктен кез-келген проекциялар жазықтығы - p₁ және проекциялау орталық нүктесі деп аталатын S нүктесін алайық (сурет 1).

p₁ жазықтығы мен S нүктесі қосылып, проекциялау аппаратын құрайды.

Кеңістіктен кез-келген А нүктесін алып, p₁ проекциялар жазықтығына оның кескінін (А₁ нүктесін) саламыз.

Сурет1

Сурет 2

Бұл үшін (сурет 1.1):

1. Кескіндеу орталық нүктесі S-тен А нүктесі арқылы SА: (SА) ' А кескіндеуші түзуін жүргіземіз;

2. SА түзуінің p₁ жазықтығымен қиылысуы А₁ нүктесі–А нүктесінің кескінін береді,, демек А: А₁ = (SА) ∩ p₁;

Кеңістікте берілген кез-келген нүктенің p₁ жазықтығындағы кескіні ұқсас тәсілмен анықталады, егер (SB) || p₁ болған жағдайда (SB) ∩ p₁ = 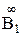. Ё және 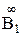Î а₁, яғни а₁ бойында жалғыз өзіндік емес 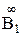нүктесі жатуы мүмкін.

S нүктесінің p₁ жазықтығына қарағандағы орналасуына байланысты проек- циялау келесі түрлерге бөлінеді:

1. Егер барлық проекциялаушы сәулелер p₁ жазықтығындағы тек бір меншікті нүкте - S арқылы өтетін болса, онда проекциялауды орталық проекциялау деп атаймыз (сурет 1.1);
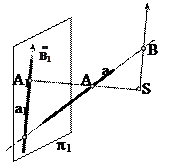
2. Егер 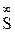шексіз қашықтықта орналасса, онда проекциялауды параллель проекциялау дейміз(сурет 2).

Сонымен қатар, параллель проекциялауды (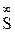А) ^ p₁ – тікбұрышты, (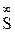А) ^ p₁ болса, қиғашбұрышты деп атаймыз.

Енді орталық және параллель проекциялауға ортақ кейбір жағдайларды атап өтейік:

1. нүктенің жазықтықтағы проекциясы нүкте болады, бірақ бір проекциялау сәулесінің (SA) бойында жатқан нүктелер А₁ нүктесіне сәйкес келеді.

2. түзудің (а) проекциясы жалпы жағдайда түзу (а₁) болады. Егер (ℓ) түзуі S: (ℓ ' S) арқылы өтетін болса, онда оның проекциясы нүктеге проекцияланады.;

3. егер А нүктесі (а) түзуінің бойында жатса, онда А₁ проекциясы да а₁ проекциясында жатады а₁: (А Î а Þ А₁ Î а₁);

4. егер (а және b) түзулері қиылысатын болса, онда олардың проекциялары (а₁ және b₁) да қиылысады: (а ∩ b = К Þ a₁ ∩ b₁ = К₁).

Параллель проекциялау үшін орынды:

5. кесінділердің ұзындықтарының қатынасы проекцияларының ұзындықтарының қатынасына тең:

.

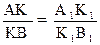6. егер түзулердің (а || c) бірі-бірімен параллель болса, олардың проекциялары да параллель: а || c Þ а₁ || c₁ Ù а₂ || c₂;

Монж тәсілі.

Монж эпюріндегі нүкте моделдері

Тікбұрышты проекциялау жағдайында жалғыз проекциялар жазықтығында бір нүктенің екі кескінін салу мүмкін емес, сондықтан проекциялар аппаратын екі еселеуге тура келеді, яғни бір проекция жазықтығының орнына өзара қиылысатын p₁ және p₂ жазықтықтары мен S₁ және S₂ проекциялау центрлерін алу қажет.

Егер p₁ және p₂ проекциялар жазықтықтарын бірін-біріне тікбұрыштап орналастырсақ, ондай жазықтықтарға тікбұрыштап проекциялауды Монж тәсілі деп атайды.

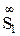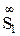S₁ және S₂ проекциялау центрлері проекциялар жазықтықтарына перпендикуляр бағытта шексіздікте орналасқан: ^ p₁; ^ p₂.

p₁ – фронталь проекциялау жазықтығы

p₂ – горизонталь проекциялау жазықтығы

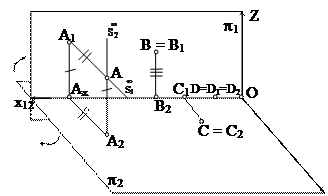
х₁₂ = p₁ ∩p₂ – проекция осі (сурет 3)

Y

Сурет 3

Сурет 4

Кеңістіктен кез-келген А нүктесін алып, оның p₁ және p₂ жазықтықтарына проекцияларын саламыз (сурет 3). Бұл үшін төмендегі шарттарды орындаймыз:

1. (S₁А) ^ p₁;

2. А₁ = (S₁А) ∩ p₁; А₁ – А нүктесінің фронталь проекциясы;

3. (S₂А) ^ p₂;

4. А₂ = (S₂А) ∩ p₂; А₂ – А нүктесінің горизонталь проекциясы.

1.4 суреттегі көрнекі сызба күрделі болғандықтан тәжірибеде сирек қолданылады. Егер осы сызбаны жазық түрге айналдыратын болсақ, онда ол едеуір жеңіл болар еді. Бұл үшін p₂ горизонталь жазықтығын x_1,2. осінен айналдырып, фронталь жазықтықпен беттестіреміз. сылай алынған проекцияны Монж эпюрі немесе кешенді сызба дейді (сурет 4).

Монж эпюрі кеңістіктің графикалық моделі болып табылады. Бұл моделде нүкте нүктеге, түзу түзуге (жалпы жағдайда), фигура фигураға кескінделінеді. Бұл моделдердің қасиеттері кеңістіктегі объектілердің қасиеттеріндей. Кеңістіктің графикалық моделдері сызба геометрия курстарында кеңірек оқытылады.

Кеңістіктің координаттық моделі әртүрлі үштік нақты сандардан(координаттардан) тұрады. Әрбір үштік санға бір ғана нүкте сәйкес болады. Кеңістіктегі объектілерді анықтайтын нүктелер жиыны үш айнымалы х, у, z шамалары бар теңдеулермен сипатталады.

Координаталар мен теңдеулер кеңістік фигуралар мен нүктелердің өзара байланысын көрсетеді: егер нүктенің координаталары фигураның теңдеуін қанағаттандыратын болса, нүкте берілген жиынға тиісті. Координаттық модельдер аналитикалық геометрияда тереңірек қарастырылады.

Есеп.Эпюрде В {B₁B₂} нүктесі В (4,2,3) координаталарымен берілген (сурет 5). Осы В нүктесінің оң жағынан p₁ және p₂ жазықтықтарына жақын орналасқан С {С₁С₂} нүктесін салайық. Анықталуы тиіс: а) С нүктелерінің координаталарын; б) В және С нүктелерінің қайсысы қараушыға жақын? в) В нүктесі p₁ және p₂ жазықтықтарының қайсысына жақын?

Сурет 5

Дата добавления: 2014-01-03