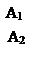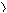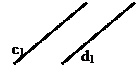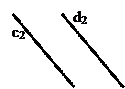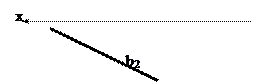КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №2
|
|
|
|
Шешуі
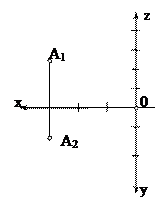
а) С нүктесінің координаталары мына шарттарды қанағаттандыруы тиіс: XC < XB, ZC < ZB, YC < YB. С нүктесінің координаталар шамасын сызба бойынша анықтаймыз: С (2,1,2).
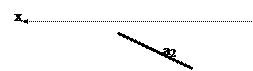
б) В нүктесі қараушыға жақын, өйткені ÷B2 BXê>÷C2 CXê.
в) В нүктесі p1 жазықтығына жақын, өйткені ÷B1 BXê>÷ВХ В2ê.
Геометриялық бейнелердің берілуі
Геометриялық элементтер аналитикалық түрде-теңдеумен, немесе графикалық түрде – анықтаушымен берілуі мүмкін.
Кеңістікте және сызбада фигураны бірмәнді түрде беретін тәуелсіз шарттардың жиынтығын анықтаушы деп атайды.
Анықтаушы екі: геометриялық элементтердің тұрақты жиынтығынан тұратын геометриялық (ГА) және тұрақты элементтерден айнымалыларғаға (үзіліссіз каркас) өтудің сипаттауын беретін алгоритмдік (АА) бөліктерден тұрады. Бір геометриялық бейне әртүрлі анықтаушымен берілуі мүмкін.
Түзу мен қисық сызықтардың және сонымен қатар жазықтықтардың анықтаушысы тек қана геометриялық болады.
Есептерді шешіңіздер:
1. А нүктесінің берілген координаталары (30, 10, 20), В (15, 0, 30), С (40, -25, 10) бойынша тікбұрышты проекцияларын салыңыздар:
1) А, В, С нүктелерінің;
2) А нүктесінің p2 жазықтығындағы вертикаль орын ауыстырудан алынған А¢ нүктесінің проекциясын;
3) p2 проекциялар жазықтығына қарағанда А нүктесіне симметриялы М нүктесінің проекциясын;
4) p1 проекциялар жазықтығына қарағанда С нүктесіне симметриялы N нүктесінің проекциясын;
Мына сұрақтарға жауап беріңіздер: 1. А немесе В нүктелерінің қайсысы бақылаушыға жақын? Бұл сұраққа жауап беру үшін, қай кесінділердің ұзындықтарын салыстыру керек? 2. С нүктесі p1 және p2 жазықтықтарының қайсына жақын? 3. Х осіне қарағанда А нүктесіне симметриялы D нүктесі кеңістіктің қай ширегінде орналасқан? А нүктесіне Х осіне дейінгі қашықтық неге тең? 4. p1 жазықтығында берілген А нүктесімен фронталь-бәсекелес В нүктесін салыңыздар. А және В нүктелерінің координаталарын анықтаңыздар. 5. p1 жазықтығына дейінгі қашықтығы p2 және p3 –ке дейінгі қашықтықтан екі есе үлкен А нүктесінің үш проекциясын салу. А нүктесінің координаталарын жазыңыздар. (6,7 – суреттер)
Сурет. 6 |
Сурет 7 |
    
      
| Көрнекі кескін бойыншаА, В, С нүктелерінің үш проекциясын салу (сурет 8.) Сурет 8. |
Түзудiң проекциялары. Монж эпюріндегі түзулердің моделдері. Түзудің түрлері
Түзудің анықтаушыларының бірі оның нүктелер жұбы болады, яғни ℓ түзуі эпюрде берілген, егер оның екі нүктесінің координаталары белгілі болса, мысалы,
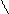
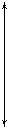            
| А (XA, YA, ZA) и В (XB, YB, ZB), онда ℓ түзуінің геометриялық анықтаушысы былай жазылады: ГА ℓ {A,B} A ¹ B (сурет 9.). С Î ℓ Þ С1 Î ℓ1 Ù С2 Î ℓ2 Ù (С1 С2) ^ х12 Сызбада түзуді (ℓ) оның екі проекциясымен (ℓ1 и ℓ2) беруге болады. Бұл жағдайда түзудің геометриялық анықтаушысы былай жазылады: ГА ℓ{ℓ1,ℓ2}. | ||||||||||||||||||||||||||
| Сурет 9. |
Бұл кезде түзудің моделі түзулер жұбы болып табылады.
Түзудің кеңістіктегі әртүрлі жағдайда орналасуы.
I.  Егер ℓ{ℓ1, ℓ2} түзуі проекциялар жазықтығына параллель немесе перпендикуляр болмаса, онда түзу кеңістікте жалпы жағдайда орналасады. Бұл жағдайда ℓ түзуінің проекциялары Х осіне параллель және перпендикуляр болмайды х ¸ ℓ1 || х1,2,
Егер ℓ{ℓ1, ℓ2} түзуі проекциялар жазықтығына параллель немесе перпендикуляр болмаса, онда түзу кеңістікте жалпы жағдайда орналасады. Бұл жағдайда ℓ түзуінің проекциялары Х осіне параллель және перпендикуляр болмайды х ¸ ℓ1 || х1,2,
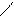
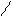 ℓ2 || х1,2, ℓ1 ^ х1,2, ℓ2 ^ х1,2, (сурет 9).
ℓ2 || х1,2, ℓ1 ^ х1,2, ℓ2 ^ х1,2, (сурет 9).
Деңгейлік түзулер – p1 немесе p2 проекциялар жазықтығының біріне параллель түзулер.
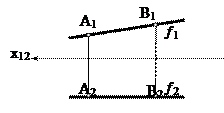
а) f {A, B} Û f {f1,f2} || p1,
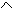
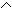 f || p1 Þ YA = YB Þ f2 || x1,2
f || p1 Þ YA = YB Þ f2 || x1,2
÷А Вê = ÷А1 В1ê Ù f p2 = f1 x1,2
|
|
|
 | |||
 | |||
| Сурет 10 | Сурет 11 |
б) h {AB} Û h {h1 h2} || p2 Þ ZA = ZB Þ h1 || x1,2 Ù ÷АВê = ÷А2В2ê;
h^p1 = h2^x1,2 ;
h {h1h2} – горизонталь түзу немесе горизонталь (сурет 11).
Проекциялаушы түзулер – p1 немесе p2 проекциялар жазықтықтарының біріне перпендикуляр түзулер.
а) n {AB} Û n {n1 n2} ^ p2 Þ XA = XB; YA = YB;
n1 ^ x1,2 Ù ÷АВê= ÷А1В1ê;
n – горизонталь-проекциялаушы түзу (сурет 12).
 |
| Сурет 12 | Сурет 13 |
б) m {AB} Û m {m1 m2} Þ XA = XB; ZA = ZB; m2 ^ x1,2
÷АВê = ÷А2В2ê;
m – фронталь-проекциялаушы түзу (сурет 13).
Профиль түзу p {AB}– p1 және p2 жазықтықтарына бірдей перпендикуляр жазықтықта жататын, бірақ р {AB} түзуінің өзі p1 немесе p2 жазықтықтарына перпендикуляр болмайтын түзу (сурет 14).
| ртүзуініңр1 және р2 проекциялары екі параметрлі жиын болуы мүмкін және бұл жиыннан жалғыз профиль түзуді бөліп алу үшін А және В нүктелерін белгілеу қажет. р {AB} || p3 Þ XA = XB Ù p1 ^ x1,2 Ù p2 ^ x1,2 | |||
| Сурет 14 |
Екі түзудің өзара орналасуы.
Түзулер кеңістікте бірі-бірімен параллель (c || d), қиылысып (a ∩ b) және айқасып (m ·¤ n) орналасуы мүмкін.
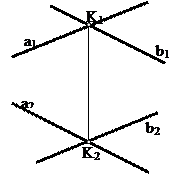
1. Егер екі түзу өзара қиылысатын болса, онда олардың аттас проекциялары да өзара қиылысады және қиылысу нүктелері бір байланыс сызығының бойында жатады: a ∩ b = k Û a1 ∩ b1 = k1 Ù a2 ∩ b2 = k2 Ù (k1k2) ^ x (сурет 1.17).
2. Параллель түзулердің аттас проекциялары да параллель болады c || d Û c1 || d1 Ù c2 || d2, (сурет 1.18).
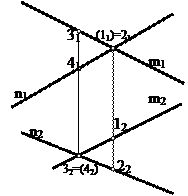
3. Айқас түзулердің аттас проекциялары қиылысады, бірақ қиылысу нүктелері бір байланыс сызығының бойында жатпайды (сурет 1.19).
Айқасатын түзулердің проекцияларынан әрқашанда бәсекелес нүктелерді, яғни бір проекциялаушы сәуленің бойында жататын нүктелерді белгілеуге болады.
 1 және 2 нүктелері – фронталь-кескіндеуші (1 ↑ 2), бұл жерде1 Î m, 2 Î n.
1 және 2 нүктелері – фронталь-кескіндеуші (1 ↑ 2), бұл жерде1 Î m, 2 Î n.
 3 және 4 нүктелері – горизонталь-бәсеклес, (3 ↓ 4), 3 Î m, 4 Î n.
3 және 4 нүктелері – горизонталь-бәсеклес, (3 ↓ 4), 3 Î m, 4 Î n.

 Бәсекелес нүктелердің проекциялары p1 немесе p2 жазықтықтарының біреуінде сәйкес болады: 1 ↑ 2 Þ 11 = 21; 3 ↓ 4 Þ 32 = 42.
Бәсекелес нүктелердің проекциялары p1 немесе p2 жазықтықтарының біреуінде сәйкес болады: 1 ↑ 2 Þ 11 = 21; 3 ↓ 4 Þ 32 = 42.
Екі бәсекелес нүктенің бақылаушыға жақын орналасқаны көрінетін болады, яғни 3 және 2 нүктелері көрінеді.
| |||||||||||||||||||||||
| Сурет 1.17 | Сурет 1.18 | Сурет 1.19 |
|
|
        
| Анализ: егер нүкте түзуге тиісті болса, онда оның проекциялары да бұл түзудің аттас проекцияларына тиісті, демек: A Î ℓ Þ A1 Î ℓ1 Ù A2 Î ℓ2 B Î ℓ Þ B1 Î ℓ1 Ù B2 Î ℓ2 C Î ℓ Þ C1 Î ℓ1 Ù C2 Î ℓ2 | ||||||||||
| Сурет 1.20 |
Шешуі:
1. A1 Î ℓ1 Ù A2 Ï ℓ2 Þ A Ï ℓ;
2. B1 Î ℓ1 Ù B2 Ï ℓ2 Þ B Ï ℓ;
3. C1 Î ℓ1 Ù C2 Î ℓ2 Þ C Î ℓ.
Есеп. Жалпы жағдайдағы ℓ {ℓ1ℓ2} түзуінің бойынан М {М1М2} Î p2 және
N {N1N2} Î p1 нүктелерін анықтау (сурет 1.22).
| Анализ:
1. M Îp2 Þ M1Îx;
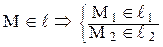 M1 = ℓ1 ∩ x
2. N Î p1 Þ N2 Î x;
M1 = ℓ1 ∩ x
2. N Î p1 Þ N2 Î x;
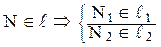 N2= ℓ2∩x
N2= ℓ2∩x
| ||||
| Сурет 1.22 |
M және N нүктелері түзудің іздері деп аталады. Ол нүктелер ℓ түзуінің p1 және p2 проекциялар жазықтықтарымен қиылысу нүктелері болып табылады:
M = ℓ ∩ p2; N = ℓ ∩ p1.
Есептерді шешіңіздер:
1. AB, CD, EF кесінділерінің проекцияларын салыңыздар:
| AB || p1 AB ^ p2 = 30° ÷АВê = 20 | CD || p2 CD ^ p1 = 60° ÷CDê = 30 | EF ^ p1 ÷EFê = 25 | ||||||||||||||||||
  
    
   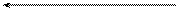
|
2. А нүктесі арқылы ℓ түзуін жүргізіңдер:
1) p1 жазықтығына параллель және а түзуімен қиылысатын;
2) b түзуіне параллель;
3) с түзуімен айқасатын.
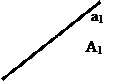 | 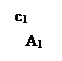 | |||||||
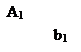 | ||||||||
 | ||||||||
| ||||||||
 
    
    
     1. 1.
| 2. | 3. | ||||||||||
| Есептердің графикалық шешу алгоритмін жазыңдар: | Сызбада түзулердің кес-кінделу ерекшеліктерін атаңдар. | Айқас түзулердің бойынан бәсекелес нүктелерді және олардың көрінетіндігін анықтаңдар. |
|
|
| 4. Кеңістіктің I, II және IV ширектері арқылы өтетін проекцияларын салыңдар. | 5. Берілген ℓ және k түзулерімен қиылысатын А нүктесі арқылы өтетін m түзуін салыңдар. | ||||||||||||||||

 

|
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1128; Нарушение авторских прав?; Мы поможем в написании вашей работы!