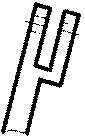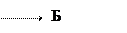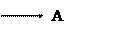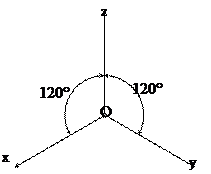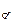Лекция №5. Проекциялық сызу. Көріністер МЕСТ 2.305-68**

Лекция

Проекциялық сызу. Көріністер МЕСТ 2.305-68**

Заттар мен бөлшектердің кескіндерін (сызбаларын) тікбұрышты проекциялау әдісімен орындайды. Сызбадағы кескіндер мазмұнына қарай көріністер, тіліктер және қималар болып бөлінеді.

Көріністердің, тіліктердің және қималардың саны мүмкіндігінше аз, бірақ заттың пішіні мен өлшемдерін көрсетуге жеткілікті болуы қажет.

Көріністер МЕСТ 2.305-68**

Көрініс дегеніміз зат бетінің бақылаушыға көрінетін бөлігінің кескіні. Кескіннің санын азайту үшін заттың көрінбейтін керекті бөліктерін штрих сызықтарының көмегімен көрсетуге болады.

Көрініс негізгі, қосымша және жергілікті болып бөлінеді.

Негізгі көріністер затты фронталь проекциялау жазықтығымен беттестірілген алты қырлы іші қуыс кубтың жақтарына тікбұрыштап проек-циялау нәтижесінде алынады.

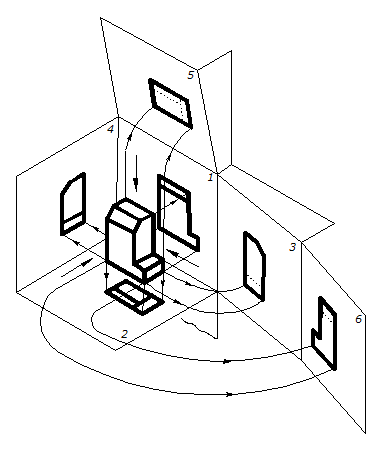
	Затты шартты түрде куб-тың ішінде орналасқан деп қарастырады (1-сурет). Зат фронталь проек-циялау жазықтығына оның пішіні мен өлшемдері туралы толық мәлімет беретіндей етіп орналастырылады. Осы кес-кінді басты көрініс (алдыңғы көрініс) деп атайды. Басқа көріністердің бас-ты көрініске қарағандағы орна-ласуын проекциялау жазық-тықтарын бір жазықтыққа жазу арқылы анықтайды (сурет 5.3).
1-сурет

Қарау бағытын орыс алфавитінің бас әріптерімен белгіленген нұсқамен көрсету қажет (2-сурет).

Стандартқа байланысты, бірінші бұрыш проекциялау әдісіне сәйкес орналаспаған көріністер (Е әдісі) немесе басқа бетке орналасқан көріністер

«А», «Б» тәріздес жазбалармен көрсетіледі (2 в, г-сурет).

    2-сурет

Егер қарау бағыты көрсетілуі мүмкін кескін жоқ болатын болса, онда көріністің атауы жазылып қойылады, мысалы: «Сол жақ көрініс», «Астыңғы көрініс» және т.б.

Құрылыс сызбаларында көріністердің өзара орналасуына қарамастан, егер қарау бағыты көріністің атауы мен белгіленуі бойынша анықталатын болса, көріністің атауы мен белгіленуін қарау бағытының нұсқамасысыз көрсетуге болады.

Көріністің саны мейлінше аз болуы, бірақ оның пішіні мен өлшемдері туралы толық мәлімет беруі керек.

		б))

а)

А

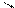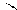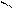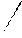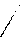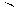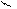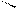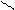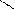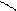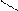
Егер заттың кейбір бөліктерінің пішіні мен өлшемдерін негізгі проекциялар жазықтығына бұрмаланусыз көрсету мүмкін болмаса, онда негізгі проекциялар жазықтықтарына параллель емес жазықтықтарда алынған қосымша көріністерқолданылады.

3-сурет

Бұл үшін қосымша көрініс сызбада «А»немесе «®А» жазбасымен белгіленеді, ал қарау бағыты нұсқамамен көрсетіледі (3 а, б-сурет).

б) а)
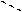
4-сурет

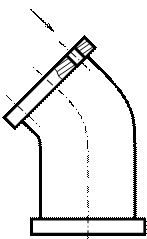
Егер қосымша көрініс тиісті кескіндермен тікелей проекциялық байланыста орналасқан болса, онда симметриялық кескін үшін көрініске жазба қойылмайды (4а-сурет), ал симметриялық емес кескіндерге қарау бағытын нұсқамамен көрсетеді (4б-сурет).

	а)	б)
5-сурет

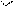
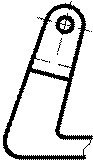
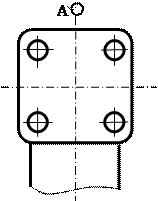
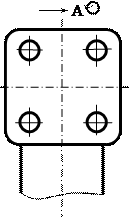
Қосымша көріністі негізгі көрініске қарағанда бұрып көрсетуге болады, мұндай жағдайда оған МЕСТ2.305-68** бойынша «» белгісі қойылады (5а, 5б-суреттер).

		Б

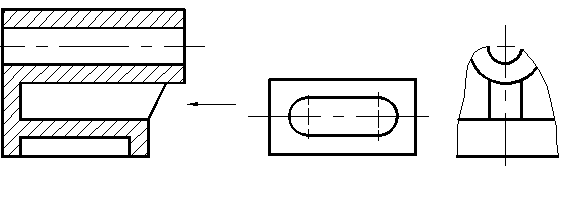
6-сурет

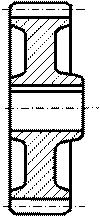
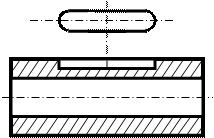
Зат бетінің шектелген бөлігінің кескінін жергілікті көрініс деп атайды. (А көрінісі, 6-сурет). Жергілікті көріністі үзік сызықтармен шектеуге болады, мүмкіндігінше өте кіші өлшемде (Б, 6-сурет).

Егер кескін біртектес болса, онда барлық көріністің орнына кескінделінетін заттың қажетті бөлігін көрсетуге болады және бұл жерде проекциялау бағыты белгіленбейді. Негізгі кескінмен жергілікті көріністің проекциялық байланысы остердің көмегімен іске асырылады (6а,б-сурет).

7-сурет

Аксонометриялық проекциялар. Стандарт

аксонометриялық проекциялар

Біз жоғарыда геометриялық фигураларды өзара екі перпендикуляр проекциялар жазықтығына ортогональ проекциялау тәсілдерімен таныстық. Мұндай жолмен алынған сызбаның маңызды кемістігі болады: ол зат туралы барлық жағдайда кеңістік көрініс бермейді.

Енді сызуды көрнекті түрде орындауға болатын әдісті қарастырайық. Оны берілген затты тікбұрышты координаталар осіне бекітуге негізделген аксонометриялық проекциялар тәсілімен алуға болады. Одан кейін затты осы остермен бірге таңдап алынған аксонометриялық проекциялар жазықтығына (картина жазықтығы) кескіндейді.

Төменде А нүктесінің аксонометриялық проекциясын p¢ картина жазықтығына салуды қарастырайық (сурет 1).

А нүктесін Охуz координаталар остері жүйесіне ендіреміз. Бұл жүйенің координаталар остерінен ℓ_x=ℓ_y=ℓ_z масштабты кесінділер - бірлік кесінділерді белгілейміз. А нүктесін хОу координаталар жазықтығына тік-бұрыштап проекциялаймыз. Сызбадан көрініп тұрғандай, А нүктесі координаталар басымен, әр буыны А нүктесінің белгілі координаталарын көрсететін ОА_хА₂А сынық сызығымен байлансты. Енді А нүктесін х, у, z остерімен бірге p¢ жазықтығына S бағытымен параллель проекциялаймыз; S бағыты координаталар остерінің ешқайсына да параллель емес.

Сурет 1

Сонда p¢ жазықтығында:

1. О¢х¢,О¢y¢,О¢z¢ – аксонометриялық остер.

2. А¢ – А нүктесінің аксонометриялық проекциясы.

3. ℓ¢_x, ℓ¢_y, ℓ¢_z – аксонометриялық бірлік кесінділер (жалпы жағдайда ℓ¢_x¹ℓ¢_y¹ℓ¢_z).

4. 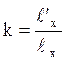;;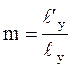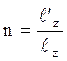қатынастары аксонометриялық остер бойынша бұрмалану көрсеткіштері деп аталады (сурет 1).

Аксонометриялық проекциялар шексіз көп. Мұны К. Полькенің (неміс геометрі 1810-1776 гг.) теоремасы дәлелдейді:

Бір жазықтықта (p¢) жататын, кез-келген ұзындығы бар бір нүктеден (О¢) шығатын, бірі-бірімен кез-келген бұрыш құрайтын, үш кесінді А¢О¢, В¢О¢, С¢О¢ бір-біріне перпендикуляр.

АО, ВО, СО кесінділерінің параллель проекциялары бола алады (сурет 2). Осы теореманы қолданып, аксо-нометриялық остер мен олардың бойынан бірлік кесінділерді қалауымызша алуымызға болады. Аксонометриялық проекциялар бұрмалану көрсеткіштерінің қатынасына байланысты келесі түрлерге бөлінеді: – триметриялық, k ¹ m ¹ n болса; – диметриялық, екі ось бойынша көрсеткіштер бірдей, мысалы k = m ¹ n болса; – изометриялық, егер k = m = n болса.

Сурет 2

Проекциялау бағытына(S) байланысты аксонометриялық проекциялар мына түрлерге бөлінеді:

- Тікбұрышты, егер S ^ p¢;

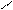- қиғашбұрышты, егер S ^ p¢.

Бұрмалану көрсеткіштері келесі тәуелділікте болады:

k² + m² + n² = 2 +ctg²j (I) – қиғашбұрышты аксонометрия үшін, j – проекциялау бағыты (S) мен картина жазықтығының (p¢) арасындағы бұрышы.

Тікбұрышты проекциялау жағдайында, яғни j=90° болғанда, (I) қатынасы мына түрде жазылады:

k² + m² + n² = 2 (II)

Тәжірибеде көп аксонометриялық проекциялардың ішінен көрнекілігі жақсы және салынуы қарапайым түрлері қолданылады. Енді солардың бірнешеуін қарастырайық.

Тікбұрышты изометрия. ГОСТ 2.317-69

Тікбұрышты изометрияда барлық координаталар остері аксонометриялық жазықтықтарға бірдей бұрышта көлбеу, сондықтан аксонометриялық остердің аралары (сурет 3) zOx = xOy = zOy = 120° және

  бұл остер бойынша бұрмалану көрсеткіштері өзара бірдей болады: k = m = n. Бұрмалану көрсеткіштерінің сандық мәндері (II) қатынасынан оңай алынады: k = m = n = 0,82. Тәжірибеде келтірілген бұрмалану көрсеткіштері k = m = n = 1 пайдаланыла ды, бұл жағдайда кескіндер 1,22:1 масштабында үлкейеді.

Сурет 3

Есеп. Берілген сызба бойынша АВ кесіндісінің тікбұрышты изометриясын салу керек. (сурет 4) АВ түзуі мен горизонталь проекция жазықтығының К қиылысу нүктесін анықтау керек.

Сызба бойынша А және В нүктелерінің координаталарын анықтаймыз (сурет 4). Алынған координаталарды қолдана отырып және k = m = n = 1 екенін ескеріп, А және В нүктелерінің тікбұрышты изометриясын саламыз (сурет 5). АВ түзуі мен p₂ жазықтығының К қиылысу нүктесі АВ түзуінің өзінің проекциясымен (А₂В₂) қиылысу нүктесі ретінде анықталады. (К = (АВ) ∩p₂ Þ К= (АВ) ∩ (А₂В₂)).

Сурет 4

Сурет 5

Шеңбер тікбұрышты изометрияда эллипске кескінделінеді. Эллипстің үлкен және кіші остерінің бағыттары мен өлшемдері шеңберлердің тиісті проекциялар жазықтығында орналасуына байланысты. Егер шеңбердің жазықтығы проекциялар жазықтығына параллель орналасса, онда эллипстің үлкен осі 1,22d, ал кіші осі – 0,7d тең болады, бұл жерде d – шеңбердің диаметрі.

O y c2 c1 z a1 z O a2 x а)	б)	в)
Сурет 6

Егер салу келтірілген координаталар бойынша жүргі-зілетін болса, онда бұл қатынастар дәл болады. Эллипстің үлкен осінің бағыты мына ереже бойынша анықталады: эллипстің үлкен осі шеңбер жазықтығына перпенди-куляр координаталар осінің кескіні болатын аксонометриялық остерге перпендикуляр болады. Ондай осьтер жазықтықта болмайды, өйткені оның кескіні нүкте болады.

Сурет 7

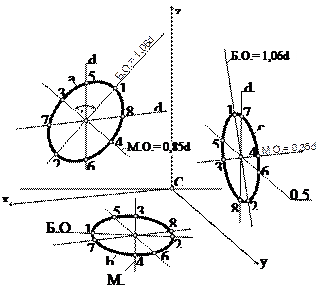
Мысалы, «b» шеңбері p₂ жазықтығында (немесе оған параллель жазықтықта) жатса (сурет 6б), онда «болмайтын» ось z және эллипстің үлкен осі z осіне перпендикуляр болады (сурет 7).

Тәжірибеде эллипсті үлкен осі-1,22d, кіші осі-0,7d тең төрт центрлі овалмен алмастырады (d – шеңбердің диаметрі).

Координаталар басын, сызбада ыңғайлы болу үшін, конус табанының центріне орналастырамыз. Сонда p₁ және p₂ проекциялар жазықтықтары ажырайды және х₁ мен х₂ остері жеке кескінделінеді. Конус табанын изометрияда саламыз: оған үлкен осі y осіне перпендикуляр болатын эллипс сәйкес, бұл жерде үлкен ось- 1,22 × d = [12], кіші ось 0,7 × d = [34] және [56] = [78] = d.

Конустың биіктігін (h) y осі бойынша өлшеп саламыз.

Тікбұрышты диметрия. ГОСТ 2.317-69

Тікбұрышты диметрия үшін бұрмалану көрсеткіштері:

k = n = 0,945, m = 0,47,

бұл жерде k - х осі бойынша бұрмалану көрсеткіші, n – z осі бойынша бұрмалану көрсеткіші, m – y осі бойынша бұрмалану көрсеткіші.

  Әдетте, келтірілген бұрмалану көр-сеткіштері қолданылады: k=n=1; m=0,5, сондықтан кескіндер үлкейтілген мас-штабта1,06:1 алынады. Аксонометриялық остердің арасындағы бұрыштар: Ð xOz = 97°10¢; Ð xOy = Ð yOz = 131°25¢.

Сурет 8

Тікбұрышты сызба бойынша А, В, С, S нүктелерінің координаталарын анықтаймыз. Бұрмалану көрсеткіштерінің х және z остері бойынша: k = n = 1 және y осі бойынша: m = 0,5 екенін ескере отырып, пирамиданың тікбұрышты диметриясын орындаймыз.

Шеңбер тікбұрышты диметрияда эллипске кескінделінеді. Егер шеңбердің жазықтығы проекциялар жазықтығына параллель болса, онда эллипстің үлкен және кіші остерінің бағыттары изометриядағы сияқты алынады.

Егера- шеңбер жазықты ғы p₁ жазықтығына параллель орналасса, онда эллипстің үлкен осі 1,06×d; кіші осі 0,95×d.тең болады. Егер шеңбер жазықтығы p₂ және p₃ жазықтықтарына параллель болса, онда үлкен ось 1,06×d; кіші ось 0,35 × d тең.

Сурет 9

Қиғашбұрышты фронталь диметрия. ГОСТ 2.317-69.

Егер p¢ картина жазықтығын фронталь проекциялар жазықтығына параллель орналастырса, онда х және z остері p¢ жазықтығына бұрмаланусыз кескінделеді, яғни Ð xOz = 90° және k = n =1.

Егер проекциялау бағытын (S) y осі бойынша бұрмалану көрсеткіші 0,5 тең болатындай етіп таңдайтын болсақ,онда алынған кескін қиғашбұрышты фронталь диметрия деп аталады, Ð z¢O¢y¢= 135°. Бұл проекцияның ұтымды қасиеті: фронталь жазықтықта орналасқан (немесе оған параллель жазықтықта) фигуралар бұрмаланусыз кескінделінеді.

Сурет 10

Дата добавления: 2014-01-03