Тема: Механическое движение. Скорость

1.1 Введение

Физика – это наука о природе. Она возникла из стремления понять и описать окружающий нас мир. Мир наш необычайно сложен и интересен: Солнце, Луна, приливы, отливы, землетрясения, день, ночь, море, облака, горы, ветер, животный и растительный мир. Человек – часть этого мира пытается понять как устроен он. Возможно ли это? Из нашего общего опыта мы знаем, что мир познаваем и что многое известно о физических законах, которые приводят к тому многообразию явлений, которые окружают нас. Физические законы образуются в результате обобщения экспериментальных данных и выражают объективные закономерности, существующие в природе.

Физика – это раздел естествознания, который изучает наиболее общие свойства и формы материи. Материя – это философская категория, изображающая объективную реальность, существующую вне сознания человека, которая отображается, копируется, фотографируется чувствами человека и существует независимо от них.

Известно два вида материи: вещество и поле. К веществу относятся, например, атомы, молекулы, и все построенные из них тела. Второй вид материи образуют электромагнитные, гравитационные поля. Эти виды материи неразрывно связаны друг с другом и могут превращаться друг в друга. Например, электрон и позитрон (представляют собой вещество) могут превращаться в фотоны (т.е. электромагнитное поле).

Механика – раздел физики, изучающий наиболее простое движение материи. Движение материи происходит в пространстве и времени, т.о. пространство и время – формы существования материи.

1.2 Механическое движение. Система отсчета. Кинематические уравнения движения

Что такое движение и как его описать? На этот вопрос отвечает кинематика, описывающая движение тел.

Механическое движение – это изменение положения тел или их частей в пространстве с течением времени относительно друг друга. Тело, по отношению к которому рассматривается движение какого-то другого тела, называется тело отсчета.

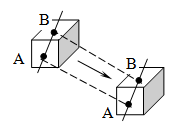
Движение тел принято разделять на несколь­ко простых видов: поступательное, вращатель­ное и колебательное.

При поступательном движении прямая, соединяющая две произвольные точки тела, перено­сится параллельно себе самой. Для изучения поступательного движения тела достаточно изучить движение какой-либо одной из его то­чек, т. к. все точки тела движутся совершенно одинаково.

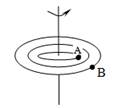
При вращательном движении тела все его точки описывают окружности в параллельных плоскостях, причем центры этих окружностей лежат на одной прямой, называемой осью вра­щения.

Колебаниями называются движения, повторяю­щиеся во времени, в окрестности некоторого поло­жения равновесия. Например, если мы подтолкнем шарик, висящий на ни­ти, то он будет совершать колебания около своего первоначального отвесного положения.

Изучение поведения тел в механике основано на двух основных моделях тел: материальной точке и абсолютно твердом теле.

Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.

Тело, конечных размеров называется абсолютно твердым, если в ус­ловиях данной задачи можно пренебречь его деформацией.

Для описания положения материальной точки вводится система координат. Совокупность тела отсчета, системы координат и часов, отсчитывающих время, называется системой отсчета. Число независимых движений, которые может совершать тело, называют числом степеней свободы. Число степени свободы – это число, которое можно задать для описания положения тел системы. Например, материальная точка имеет три степени свободы если она двигается в пространстве: поступательное движение вдоль оси x, y, z; при движении на плоскости достаточно две координатные оси, следовательно в этом случае число степеней свободы равно двум, а при движении вдоль прямой – число степеней свободы равно одному.Абсолютно твердое тело может обладать тремя степенями свободы поступательного движения, тремя степенями свободы вращательного движения, если тело не абсолютно твердое и его части могут смещаться друг относительно друга, то необходимо вводить еще дополнительные три степени свободы колебательного движения.

Выбор системы отсчета позволяет описать движение рассматривае­мых тел. Координаты – это функции времени:

x(t) = x; y(t) = y; z(t) = z (1.1)

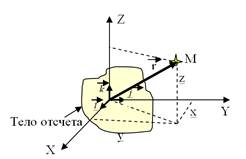
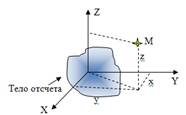
Уравнения (1), с помощью которых можно предсказывать положение точки, называется кинематическим уравнениемдвижения тела.

Если указать не только начальное положение точки, но и указать направление движения, то задача упрощается (вместо трех уравнений – получится одно уравнение):

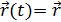(1.2),

где 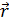- радиус вектор, проведенный из начала координат в точку М.

Уравнения (1) и (2) равносильны. Если ввести единичные векторы характеризующие направление осей координат, то положение точки можно выразить через данные вектора.

Свойства векторов: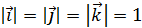

, ,

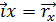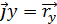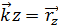
Сумма трех векторов: 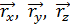равна радиус-вектору :

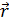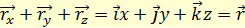(1.3)

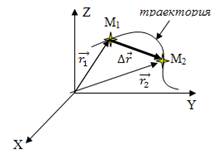
Линия, описывающая движение тела, называется траекторией. Длина траектории от точки М₁до точки М₂ – это путь. Путь 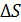– это скалярная физическая величина равная сумме длин отрезков траектории. Вектор, соединяющий начальное положение тела с конечным, называется перемещением .

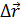Модуль малого приращения равен длине соответствующей ему дуги траектории:

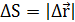или

В зависимости от формы траектории различают прямолинейное и криволинейное движения точки.

1.3 Скорость

Для характеристики движения материальной точки вводят векторную физическую величину – скорость.

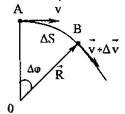
Пусть материальная точка движется по криволинейной траектории так, что в момент t₁ она находилась в точке М₁, а в момент времени 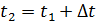в точке М₂

При движении материальной точки относительно системы отсчета меняется направление перемещения:

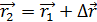
Время, потраченное на перемещение :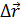

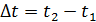
Вектором средней скорости называют отношение приращения 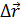радиус-вектора точки за интервал времени Δ t к его величине:

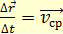(1.4)

Если известно 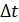и, то можно найти перемещение точки:

Вектор средней скорости характеризует только быстроту движения материальной точки за минимальный промежуток времени. Направление вектора совпадает с направлением перемещения 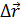. Если в выражении (1.4) перейти к пределу, устремляя 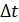к нулю, то получим выражение для мгновенной скорости:

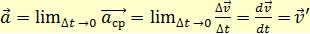(1.10)

Ускорение измеряется в м/с².

Ускорение, характеризующее изменение скорости по модулю, называется тангенциальным ускорением:

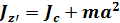
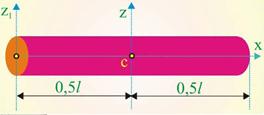
Рассмотрим момент инерции стержня, если ось вращения проходит через один из концов стержня Z₁, если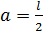

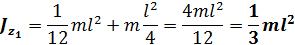
4. Закон сохранения момента импульса

Из основного закона динамики вращательного движения можно получить закон сохранения момента импульса.

Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

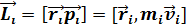(6)

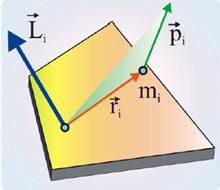
Моментом импульса абсолютно твердого тела относительно оси есть сумма моментов импульса отдельных материальных точек:

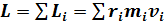(7)

Направление вектора момента импульса определяется по правилу правого винта. Единицы измерения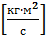

Так как связь линейной и угловой скорости: 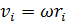, то

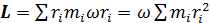(8)

Так как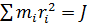то

Момент импульса:

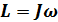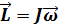или (9)

Дата добавления: 2014-01-03