
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способов обработки почвы, ц/га
|
|
|
|
Поделяночная урожайность пшеницы в опыте с изучением
| Вариант | Урожай по повторениям (Х) | Сумма по вариантам
(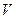 ) )
| Средняя по вариантам
(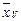 ) )
| |||
| I | II | III | IV | |||
| 13,1 | 14,6 | 16,0 | 12,3 | 56,0 | 14,0 | |
| 16,2 | 15,9 | 15,7 | 16,2 | 64,0 | 16,0 | |
| 17,3 | 18,2 | 17,7 | 17,8 | 71,0 | 17,8 | |
| 12,4 | 15,3 | 16,2 | 16,2 | 59,6 | 14,9 | |
| Сумма по повторениям (Р) | 59,0 | 64,0 | 65,1 | 62,5 | ∑Х=250,6 | |
Средняя по повторениям ( р) р)
| 14,8 | 16,0 | 16,3 | 15,6 |  о=15,7 о=15,7
|
2-й этап:. Составляют вспомогательную расчётную таблицу отклонений поделяночных урожаев Х от среднего урожая по опыту 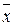 о (Х-
о (Х- о), отклонений средних по вариантам
о), отклонений средних по вариантам 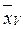 от
от  о (
о (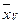 -
-  о) и средних по повторениям
о) и средних по повторениям  р от
р от  о (
о ( р-
р- о). Находят суммы отклонений по вариантам ∑(
о). Находят суммы отклонений по вариантам ∑(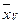 -
-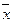 о), повторениям ∑(
о), повторениям ∑( р-
р- о) и общую сумму отклонений ∑(Х-
о) и общую сумму отклонений ∑(Х- о). При правильных вычислениях ∑(
о). При правильных вычислениях ∑(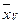 -
- о)= ∑(
о)= ∑( р-
р- о)= ∑(Х-
о)= ∑(Х- о). Затем все полученные отклонения возводят в квадрат, заносят в правую часть таблицы (таблицу квадратов отклонений) и подсчитывают суммы квадратов отклонений ∑(
о). Затем все полученные отклонения возводят в квадрат, заносят в правую часть таблицы (таблицу квадратов отклонений) и подсчитывают суммы квадратов отклонений ∑(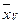 -
- о)2, ∑(
о)2, ∑(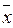 р-
р- о)2 и ∑(
о)2 и ∑( -
-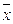 о)2.
о)2.
Таблица отклонений и квадратов отклонений от 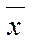 о
о
| Вариант | Отклонения (Х- о) о)
| Отклонения
(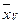 - - о) о)
| Квадраты
отклонений
(Х- о)2 о)2
| Квадраты отклонений
(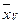 - - о)2 о)2
| ||||||
| I | II | III | IV | I | II | III | IV | |||
| -2,6 | -1,1 | 0,3 | -3,4 | -1,7 | 6,76 | 1,21 | 0,09 | 11,56 | 2,89 | |
| 0,5 | 0,2 | 0,0 | 0,5 | 0,3 | 0,25 | 0,04 | 0,00 | 0,25 | 0,09 | |
| 1,6 | 2,5 | 2,0 | 2,1 | 2,1 | 2,56 | 6,25 | 4,00 | 4,41 | 4,41 | |
| -3,3 | -0,4 | 0,0 | 0,5 | -0,8 | 10,89 | 0,16 | 0,00 | 0,25 | 0,64 | |
( р- р- о) о)
| -0,9 | 0,3 | 0,6 | -0,1 | 0,81 | 0,09 | 0,36 | 0,01 |
3-й этап: Вычисляют суммы квадратов отклонений для разных видов варьирования.
а ) Общее варьирование Су характеризуется суммой квадратов отклонений поделяночных урожаев Х от среднего урожая по опыту  о:
о:
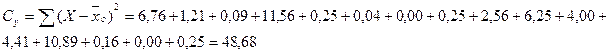
б) Варьирование по повторениям 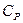 равно сумме квадратов отклонений средних урожаев по повторениям
равно сумме квадратов отклонений средних урожаев по повторениям 
 р от среднего по опыту
р от среднего по опыту 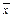 о, умноженной на число вариантов:
о, умноженной на число вариантов:
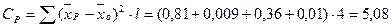
в)Варьирование по вариантам 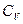 равно сумме квадратов отклонений средних урожаев по вариантам
равно сумме квадратов отклонений средних урожаев по вариантам 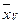 от среднего урожая по опыту
от среднего урожая по опыту  о, умноженной на повторность в опыте:
о, умноженной на повторность в опыте:
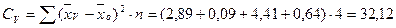
Случайное (остаточное) варьирование 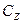 определяется по разности
определяется по разности 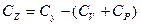
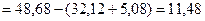
4-й этап: Определяют степень влияния каждого из факторов в отдельности на изучаемый признак (урожай), принимая общее варьирование (дисперсию) за 1 или 100%:
влияние вариантов -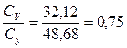 (75%);
(75%);
влияние повторений - 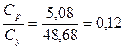 (12%);
(12%);
влияние случайных факторов - 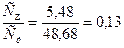 (13%).
(13%).
Если на долю варьирования вариантов по сравнению с влиянием случайных ошибок приходится наибольший процент, как в данном примере, то расчёты нужно продолжить дальше и установить существенность влияния изучаемых факторов на урожай. Когда величина 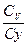 <
<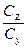 , это значит, варьирование урожаев по вариантам в основном обусловлено влиянием случайных факторов. В этом случае расчёты можно не продолжать.
, это значит, варьирование урожаев по вариантам в основном обусловлено влиянием случайных факторов. В этом случае расчёты можно не продолжать.
5-й этап:. Составляют таблицу дисперсионного анализа, в которую заносят значения различных видов варьирования, вычисляют степени свободы этих варьирований, дисперсию вариантов, дисперсию ошибок и отношение этих дисперсий, т.е. фактическое значение критерия Фишера Fфакт
Число степеней свободы равно:
Для общей дисперсии (варьирования) – 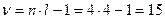 ;
;
для дисперсии повторений – 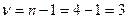 ;
;
для дисперсии вариантов – 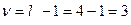 ;
;
для остаточной дисперсии – 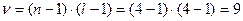 .
.
Таблица дисперсионного анализа
| Виды варьирования | Их значения | Степени свободы υ | Дисперсия S2 Ср. квадрат | Критерий Фишера | |
| Fфакт. | F05 | ||||
| Общее Су Повтор-й Ср Вариантов Ср Cлучайное Сz (остаточное) | υ = n ×ℓ - 1 υ = n – 1 υ = ℓ - 1 υ=(n-1)×(ℓ-1) | ― ― S2v= Cv : υv S2z= Cz: υz | Fф= S2v: S2z | F05 |
Не все средние квадраты (дисперсии) представляют интерес для оценки результатов опыта. Наиболее важными из них являются дисперсии вариантов 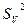 и ошибок
и ошибок 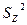 . Первая характеризует варьирование урожаев. Равенство их проверяется по критерию
. Первая характеризует варьирование урожаев. Равенство их проверяется по критерию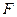 :
:
дисперсия вариантов –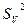 =
= 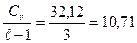 ;
;
дисперсия ошибок - 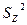 =
= 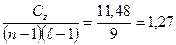 ;
;
значение критерия – 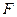 =
= 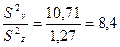 .
.
Теоретическое значение критерия 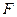 для принятого уровня значимости (05 или 01) находят по прил. 3 и 4 при числе степеней свободы для дисперсии вариантов
для принятого уровня значимости (05 или 01) находят по прил. 3 и 4 при числе степеней свободы для дисперсии вариантов 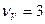 и дисперсии ошибок
и дисперсии ошибок 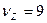 .
.
Заключение по критерию Фишера (F)
По критерию 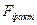 устанавливают наличие в опыте вариантов, имеющих существенные разности урожаев. Наличие в опыте вариантов с существенной прибавкой или снижением урожая подтверждается, когда
устанавливают наличие в опыте вариантов, имеющих существенные разности урожаев. Наличие в опыте вариантов с существенной прибавкой или снижением урожая подтверждается, когда 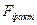 ≥
≥ 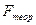 . Если
. Если 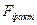 <
< 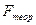 , то между средними по вариантам нет существенных различий, т.е. различия между вариантами находятся в пределах ошибки опыта или в опыте имеет место нулевая гипотеза – Но. В этом случае оценку частных различий (между средними по вариантам не проводят. При
, то между средними по вариантам нет существенных различий, т.е. различия между вариантами находятся в пределах ошибки опыта или в опыте имеет место нулевая гипотеза – Но. В этом случае оценку частных различий (между средними по вариантам не проводят. При 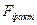 ≥
≥ 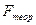 дают оценку существенности частных различий по критерию
дают оценку существенности частных различий по критерию 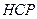 .
.
6-й этап: На этом этапе оценивают существенность разности (частных различий). Под частными различиями понимают разности между средними урожаями опытных вариантов и контролем, а также разности средних урожаев опытных вариантов между собой.
Количество этих разностей находят: d = ℓ×(ℓ - 1): 2 = 4×(4 – 1): 2 = 6
= 4×(4 – 1): 2 = 6
d1 = х2 – хк
d2 = х3 – хк
d3 = х4 – хк
d4 = х3 – х2 Эти разности называются частными различиями
d5 = х4 – х2
d6 = х4 – х3
Чтобы доказать существенность этих различий, рассчитывают ещё три вида показателей:
1. Ошибка опыта в абсолютных величинах:
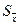
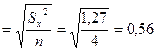 ц;
ц;
2. Ошибка разности средних:
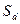
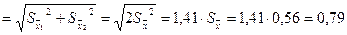 ц
ц
3. Наименьшая существенная разность 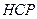 для принятого уровня значимости 05:
для принятого уровня значимости 05:
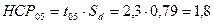 ц,
ц,
Значение критерия 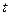 находим по прил. 2 по числу степеней свободы для остаточной (случайной) дисперсии
находим по прил. 2 по числу степеней свободы для остаточной (случайной) дисперсии 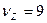
Заключение. Разность между средними 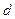 считается существенной, когда
считается существенной, когда 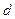 ≥
≥ 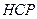 . Если
. Если 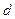 <
< 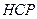 , разность несущественная, т.е. она не выходит за пределы ±
, разность несущественная, т.е. она не выходит за пределы ±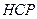 и, следовательно, находится в пределах ошибки опыта. В данном примере при 5%-ом уровне значимости прибавки урожаев во втором и третьем вариантах существенны.
и, следовательно, находится в пределах ошибки опыта. В данном примере при 5%-ом уровне значимости прибавки урожаев во втором и третьем вариантах существенны.
Урожайность в варианте с осенней плоскорезной обработкой почвы на 20-22 см (вариант 2) составила 16,0 ц/га, в варианте с осенней вспашкой на 20-22 см (контроль) – 14,0 ц/га. Разница (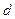 ) между урожайностями 2,0 ц/га и она превышает
) между урожайностями 2,0 ц/га и она превышает 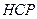 05=1,8 ц/га. Урожайность в варианте с осенней плоскорезной обработкой на 10-12 см (вариант 3) по сравнению с контролем выше на 3,8 ц/га, что тоже превышает
05=1,8 ц/га. Урожайность в варианте с осенней плоскорезной обработкой на 10-12 см (вариант 3) по сравнению с контролем выше на 3,8 ц/га, что тоже превышает 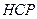 05.
05.
Дисперсионный анализ с применением корректирующего фактора (модель 2-я)
Одним из методов расчёта сумм квадратов отклонений для разных видов варьирования является способ произвольного начала. Применяется он при обработке многозначных цифр и отсутствии счётных машин. Сущность его заключается в том, что отклонения поделяночных урожаев Х находят не от среднего урожая по опыту 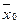 (как уже было рассмотрено), а от условной средней величины А (произвольного начала). За условную среднюю берут любое целое число, близкое к среднему урожаю по опыту. Это значительно упрощает вычисление отклонений и сводит ошибки при расчётах к минимуму. Технику расчёта рассмотрим на том же самом примере
(как уже было рассмотрено), а от условной средней величины А (произвольного начала). За условную среднюю берут любое целое число, близкое к среднему урожаю по опыту. Это значительно упрощает вычисление отклонений и сводит ошибки при расчётах к минимуму. Технику расчёта рассмотрим на том же самом примере
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1285; Нарушение авторских прав?; Мы поможем в написании вашей работы!