Нахождение оценки для коэффициента корреляции двух случайных величин

Пусть над системой СВ 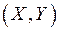произведено в одинаковых условиях 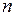независимых опытов. Результаты опытов:

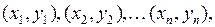(13)

являются независимыми системами СВ, матожидания, дисперсии, корреляционные моменты которых одинаковы:

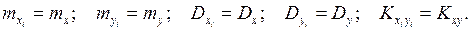
Требуется на основании статистических данных (13) найти оценки этих числовых характеристик системы. Для математических ожиданий и дисперсий компонент системы 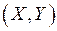имеем известные формулы для их оценок:

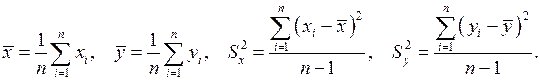(14)

Так как корреляционный момент равен: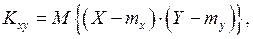

будем искать оценку для него 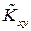в виде:

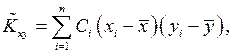(15)

причем в силу равноточности измерений 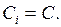Неизвестный коэффициент 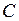определяется из условия несмещенности оценки (15).

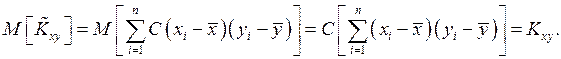
После преобразования выражений, стоящих под знаком суммы, получим несмещенную, состоятельную оценку для корреляционного момента:

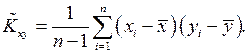(16)

Выборочный коэффициент корреляции определяется по формуле:

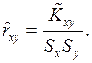(17)

Вместо формул (16) и (17) для выборочного коэффициента корреляции полезно иметь расчетные формулы, использующие статистические данные (13). Имеем:

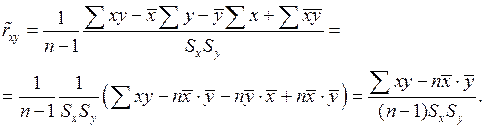
Таким образом, для выборочного коэффициента корреляции имеем следующую формулу:

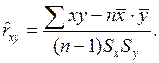(18)

Если использовать вместо «исправленных» выборочных дисперсий 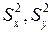выборочные дисперсии 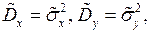то с использованием формулы их связи: 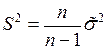вместо формулы (18) получим:

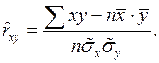(19)

Выборочный коэффициент корреляции 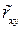является оценкой коэффициента корреляции .

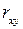Пример 2.Используя данные в примере 1., найти выборочные коэффициенты корреляции.

Решение:

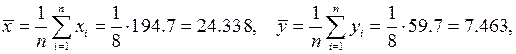
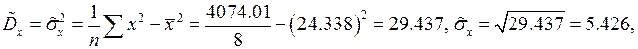
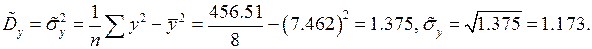
Используя формулу (19) имеем:

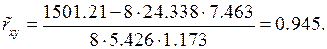
Дата добавления: 2014-01-03; Просмотров: 288; Нарушение авторских прав?; Мы поможем в написании вашей работы!