Распределение Стьюдента

Пусть Z – случайная величина, имеющая нормальное распределение N(0,1), а V – независимая от Z случайная величина, распределенная по закону c² с n степенями свободы. Введем случайную величину:

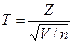. (28)

Тогда соответствующая этой случайной величине плотность распределения имеет вид: 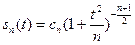, где

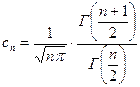. (29)

Распределение, определяемое функцией плотности s_n (x), известно под названием распределения Стьюдента или t-распределения. Оно было впервые использовано в одной важной статистической проблеме В.Госсетом, писавшим под псевдонимом “Стьюдент” (Student). Как и в случае c²-распределения, параметр n часто называют числом степеней свободы t-распределения. Нетрудно убедиться, что это распределение унимодально и симметрично относительно x = 0. При n< n моменты n-го порядка конечны. В частности, математическое ожидание конечно при n >1, а стандартное (среднеквадратическое) отклонение – при n >2. Вследствие симметричности распределения все существующие моменты нечетного порядка равны нулю. Нетрудно показать, что 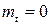, 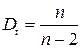(n > 2). Для больших значений n величина T асимптотически нормальна с параметрами (0,1) в соответ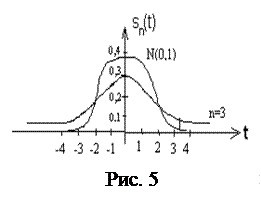ствии с соотношением 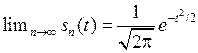. Для небольших значений n t -распределение заметно отличается от предельного нормального распределения. График распределения Стьюдента для n = 3 вместе с приведенной для сравнения нормальной кривой дан на рис. 5.

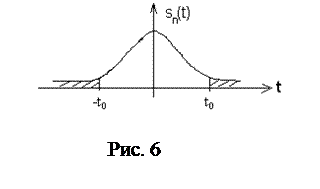Вероятность того, что величина T отличается по модулю более чем на заданную величину 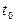от своего математического ожидания (равного нулю), равна площади заштрихованной области на рис. 6. В силу симметрии t-распределения она равна 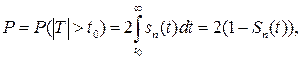где 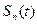– функция распределения этой случайной величины. Исходя из этого, можно табулировать t ₀ как функцию вероятности P. Если 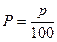, то соответствующее t ₀ = t_p называется р-процентным значением или р-процентным квантилем распределения. Численные значения этой функции даны в таблице.

Дата добавления: 2014-01-03