Применение теорем умножения и сложения вероятностей к расчету надежности систем

Теорем о повторении опытов (формула Я. Бернулли).

Формула Байеса (теорема гипотез).

Формула полной (средней) вероятности.

Применение теорем умножения и сложения вероятностей к расчету надежности систем.

Лекция №3

Раздел 1. Основанные понятия и основные законы теории вероятностей.

Тема 2. Основные законы теории вероятностей.

Цель лекции: дать знания об основных законах теории вероятностей.

Вопросы лекции:

Литература:

Л1 - Бочаров П. П., Печинкин А. В. Теория вероятностей. Математическая статистика. - 2-е изд. - М.: ФИЗМАТЛИТ, 2005. - 296 с.

Л2 - Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2005. — 479 с: ил.

Л3 - Нахман А.Д., Косенкова И.В. Ряды. Теория вероятностей и математическая статистика. Методические разработки. – Тамбов: Издательство ТГТУ, 2009.

Л4 - Плотникова С.В. Математическая статистика. Методические разработки. – Тамбов: Издательство ТГТУ, 2005. (pdf-файл)

Надежностью системы называется ее способность выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки. Это определение характеризует систему с качественной стороны. Одним из основных количественных показателей надежности системы является вероятность Р(t) безотказной работы за время t, которая представляет собой вероятность того, что система проработает безотказно в течение времени t, начав работать в момент времени t = 0, или вероятность того, что время работы системы до отказа Т окажется больше заданного времени работы t: P(t)= P(T>t).

При объединении нескольких элементов в систему различают их последовательное (основное), параллельное (резервное) и смешанное соединения.

Соединение элементов в систему называется последовательным (рис. 1.16), если отказ системы происходит при отказе любого ее элемента.

Вычислим вероятность Р= Р(t) безотказной работы системы при последовательном соединении элементов. Пусть известны надежности p_i(t)= p_i, i= 1, 2,…,n каждого элемента, а отказы элементов независимы. Тогда события, состоящие в безотказной работе элементов, также независимы. Согласно определению, надежная работа системы (событие А) представляет собой произведение событий А_i, состоящих в безотказной работе каждого элемента: A= A₁A₂…A_n.

Так как события A₁,A₂,…,A_n независимы, то в соответствии с теоремой умножения будем иметь

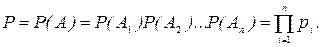(1.14.1)

Из выражения (1) видно, что с увеличением числа элементов в системе, надежность системы уменьшается, причем вероятность безотказной работы системы при последовательном соединении элементов всегда ниже, чем вероятность безотказной работы самого ненадежного элемента.

Соединение элементов в систему называется параллельным (рис. 1.17), если отказ системы происходит при отказе всех ее элементов.

Для определения надежности системы при параллельном соединении элементов в систему рассмотрим следующие события: 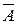- отказ системы; 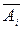- отказ i -го элемента, 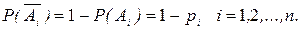Очевидно, что 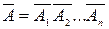. Так как события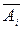, i= 1,2,…,n - независимы, то по теореме умножения получим

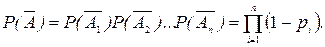
Безотказная работа системы является событием А, противоположным отказу. Поэтому

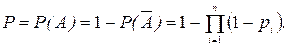(1.14.2)

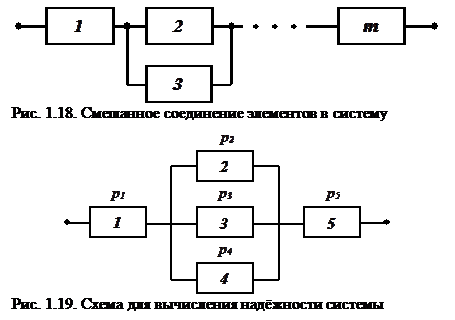Формула (2) показывает, что с увеличением числа элементов в системе надежность системы при параллельном соединении увеличивается, причем вероятность безотказной работы системы превышает вероятность безотказной работы любого элемента, в том числе и самого надежного. При резервировании структура системы усложняется. Поэтому на практике применяют не поэлементное резервирование, а поблочное, при котором надежность хотя и ниже, чем при поэлементном резервировании, но выше, чем при резервировании всей системы.

Смешанное соединение элементов представляет собой такое соединение, которое состоит из различных комбинаций последовательного и параллельного соединений элементов (рис. 1.18).

Воспользовавшись формулами (I) и (2), можно рассчитать надёжность смешанной системы.

В заключение отметим два обстоятельства. Во-первых, вероятности безотказной работы элементов берутся или из прошлого опыта эксплуатации, или оцениваются с помощью проведения испытании элементов на надежность. Во-вторых, когда отказы элементов происходят в случайные моменты времени и среднее значение числа отказов одинаково для равных по длительности периодов работы, надежность определяется экспоненциальной формулой

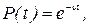(1.14.3)

где n - постоянная, называемая интенсивностью внезапных отказов, t - произвольное время работы, для которого определяется надежность. Формула (3) справедлива для периода нормальной эксплуатации при n=const, т.е. когда объекты прошли надлежащую приработку и на которые еще не сказывается изношенность, т.е. старение.

Дата добавления: 2014-01-03