Метрические задачи

Перпендикулярность прямой и плоскости.

Взаимное положение двух плоскостей, прямой и плоскости. Перпендикулярность.

Лекция 5

Система регулируемой активации

План лекции:

5.1. Перпендикулярность прямой и плоскости. Метрические задачи

5.2. Перпендикулярность двух прямых

5.3. Взаимно-перпендикулярные плоскости

5.4. Вопросы для самоконтроля

Для того, чтобы прямая в пространстве была перпендикулярна к плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонталь плоскости, а фронтальная проекция – к фронтальной проекции фронтали этой плоскости.

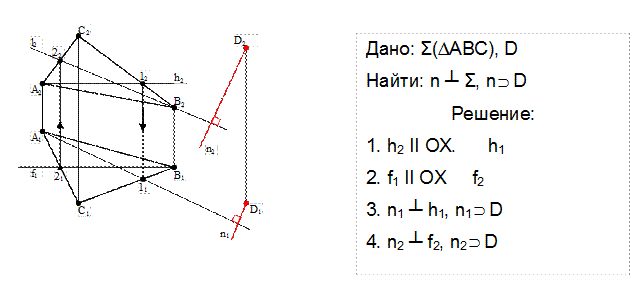
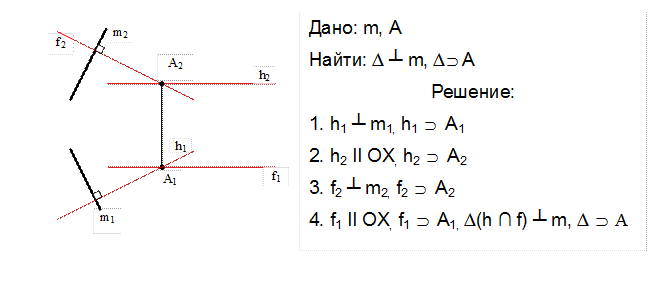
Положение о перпендикулярности прямой и плоскости позволяют решать задачи как позиционные, так и метрические. Метрические задачи заключаются в определении расстояний и углов между геометрическими фигурами.

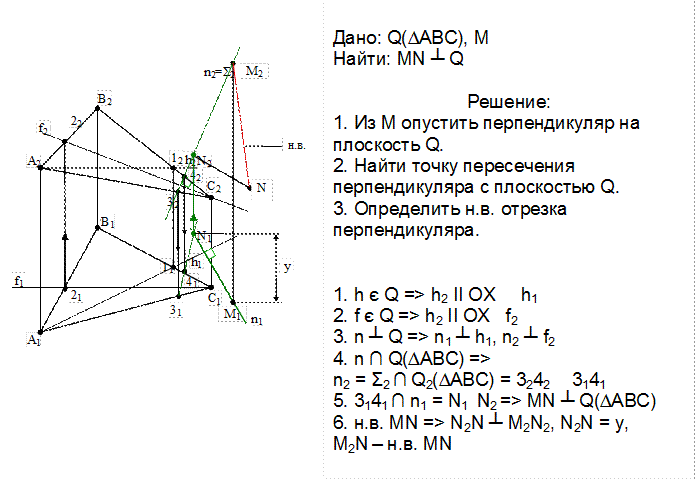
Задачи на определение расстояния между параллельными плоскостями или расстояние от прямой до параллельной ей плоскости сводятся к предыдущей. При этом в плоскости или на прямой берется точка и определяется расстояние от нее до плоскости.

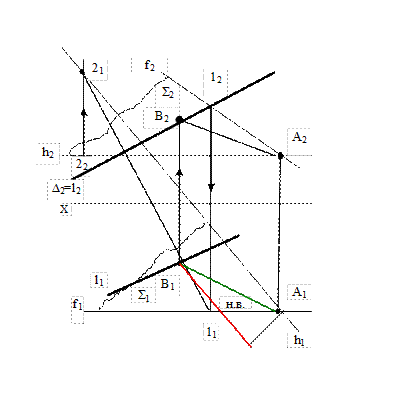
Дано: l, A

Найти: AB ┴ l

Решение

1.Через точку А провести плоскость ┴ прямой l.

2.Найти точку пересечения прямой l с построенной плоскостью.

3.Соединить точку А с полученной точкой пересечения

4.Определить н.в. полученного отрезка.

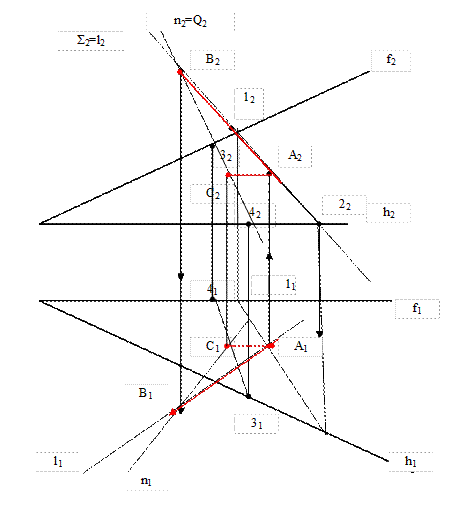
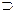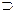I. Σ(h ∩ f) ┴ l h A f A

1.h₁ ┴ l₁ h₂ II OX

2.f₂ ┴ l₂ f1 II OX

II. l ∩ Σ=B

1. l₂=∆₂ → 1₂2₂ ↓ 1₁2₁

2. 1₁2₁ ∩ l₁=B₁ ↑ B₂

III. A U B → A₁B₁, A₂B₂

IV. н.в. AB

1.угол B₁A₁A₀=90º

2.A₁A₀=∆z → B₁A₀

При определении расстояния между параллельными прямыми на одной из прямых выбирается произвольно точка и определяется расстояние от точки до прямой (см. предыдущую задачу).

Задача по определению угла между прямой и плоскостью

Дано: ∆ (h ∩ f), l

Найти: l^∆

Решение:

1. Определение точки пересечения «А» прямой «l» с плоскостью ∆ (h ∩ f)

2. Проведение перпендикуляра «n» к плоскости ∆ (h ∩ f) из произвольной точки «B», взятой на прямой «l».

3. Определение точки «С» пересечения перпендикуляра «n» с плоскостью ∆ (h ∩ f)

4. Соединение точек А, B, С. Искомый угол BАC.

I. l ∩ ∆ (h ∩ f) =A

1.l₂=Σ₂ → 1₂2₂ ↓ 1₁2₁

2.1₁2₁ ∩ l₁=A₁ ↑ A₂

II. n ┴ ∆ (h ∩ f)

1. Точка B - произвольно B є l→ B₂ ↓ B₁.

2. n₁┴ h₁, n₂ ┴ f₂ n₁ є B₁ n₂ є B₂

III n ∩ ∆ (h ∩ f)=C

1. n₂=Q₂ → 3₂4₂ ↓ 3₁4v

2. 3₁4₁ ∩ n₁=C₁ ↑ C₂

IV.

1. A U B U C → BАC=l^∆ (h ∩ f)

Дата добавления: 2014-01-03