Математические модели объектов на макроуровне

Основными методами создания ММ на макроуровне являются инвариантные методы. Они предполагают разбиение всей систе-мы на отдельные элементы, описание свойств каждого элемента на уровне взаимодействия их между собой с помощью ММ и по-следующее объединение их в единую структуру на основе связей между однотипными фазовыми переменными. Обычно процедура выделения элементов выполняется человеком, а составление об-щей системы уравнений для полученной структуры объекта воз-лагается на ЭВМ.

Математические модели элементов получают одним из способов, рассмотренных выше. Уравнения, входящие в ММ элемен­тов, называются компонентнымы. Они отражают законы функцио-нирования элемента и связывают, как правило, разнородные фа-зовые переменные, относящиеся к этому элементу. Так, уравне-ние второго закона Ньютона связывает силу и ускорение. Уравне­ния могут быть алгебраическими или дифференциальными, линейными или нелинейными.

Для объединения элементов в систему используются топологи-ческие уравнения. Они отражают способ связи элементов между собой в составе системы. Топологические уравнения могут выражать законы сохранения, условия неразрывности, равновесия и т. п. Например, уравнения равновесия (принцип Д 'Аламбера) устанавливают, что сумма сил (моментов), действующих на тело с учетом инерционных, равна нулю. Топологические уравнения свя­зывают однотипные фазовые переменные, относящиеся к разным

элементам системы. Их получают на основе сведений о структуре системы.

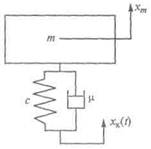
Рис. 2.3. Схема одномассо­вой динамической системы

Рассмотрим пример одномассовой колебательной системы. Пусть требуется, например, определить верти-кальные ускорения на месте водителя транспортного средства, если извес-тен закон вертикального перемещения кузова (остова) в месте установки под-рессоренного сиденья. Задача может быть решена с использованием одно­массовой схемы динамической систе­мы, показанной на рис. 2.3. Здесь мас­са сиденья и водителя т выделена в

отдельный инерционный элемент, связанный с внешней средой посредством двух элементов, учитывающих упругие с и демпфи-рующие ц. свойства сиденья. Рассмотрим движение системы вдоль вертикальной оси х, совершающей перемещение в горизонтальном направлении совместно с кузовом (остовом).

Фазовыми переменными для инерционного элемента являются сила инерции Р_т и перемещение х_т, а компонентное уравнение имеет вид

F_т = тd²х_т/dt²,

где t — текущее время (независимая переменная).

Для упругого элемента фазовыми переменными являются сила упругости Р_с и деформация А, а компонентное уравнение имеет вид

F_с = с∆.

Здесь внутренний параметр с — жесткость упругого элемента.

Фазовыми переменными элемента сопротивления будут сила сопротивления амортизатора F_я и скорость деформации d∆ /dt, а внутренним параметром — коэффициент демпфирования μ. Ком­понентное уравнение имеет вид

F_R = μd∆/dt.

Источником колебаний системы являются вертикальное пере­мещение кузова х_к (фазовая переменная источника), закон изме-нения которого известен: х_к = х_к(t).

Для получения ММ объекта необходимо полученные компо-нентные уравнения дополнить топологическими. Согласно схеме динамической системы (см. рис. 2.3) и принципу Д'Аламбера

F_т +F_с+ F_R = 0.

Из уравнения непрерывности

∆ = х_к — х_т.

Решение системы этих уравнений при выбранных значениях коэффициентов и законе перемещения кузова позволяет опреде-лить вертикальное ускорение на месте водителя а_т = d²х_т/dt² для любого момента времени.

В качестве фазовой переменной в механических системах часто используется не перемещение, а скорость, поэтому компонентные и топологические уравнения рассматриваемой системы могут иметь несколько иной вид.

В используемых САПР методах формирования ММ объектов принято моделируемую систему представлять в виде совокупнос-ти физически однородных подсистем. Каждая из них описывает процессы определенной физической природы, например механические, гидравлические, тепловые, электрические. Важно, что фор­ма компонентных и топологических уравнений одинакова для большинства из них, что объясняется наличием аналогий между раз-нородными физическими подсистемами. Подобные аналогий за-мечены давно и широко используются в науке и технике для ана-лиза объектов. Установление аналогий важно для эффективного использования САПР, так как позволяет использовать одни и те же математические методы для решения многих проектных задач с разным физическим содержанием. Аналогий дают возможность повысить степень универсальности многих элементов САПР, в частности программного обеспечения. Важно это и с методологи-ческой точки зрения, так как обусловливает возможность изложения вопросов моделирования различных технических объектов с единых позиций.

Использование аналогий предполагает, что для описания со-стояния одной подсистемы достаточно использовать фазовые переменные двух типов, а в большинстве технических объектов можно вьщелить три типа простейших элементов: элемент диссипации, преобразующий энергию соответствующего данной подсистеме вида в теплоту, и элементы, накапливающие потенциальную или кинетическую энергию.

Аналогию компонентных и топологических уравнений удобно проводить на основе электрической подсистемы. Рассмотрим ис­пользование аналогий на примерах подсистем, наиболее харак-терных для автомобиля и трактора — механической, гидравлической (пневматической), тепловой и электрической.

Электрическая подсистема. Типовыми простейшими элемента-ми электрической подсистемы являются электрическое сопротивление R, электрическая емкость Си электрическая индуктивность L. При описании их функционирования используются фазовые пе-ременные типа потока (сила тока I) и типа потенциала (напряжение U ). Значение напряжения на этих элементах совпадает с раз ностью значений электрического потенциала на концах элемен­тов, напряжение на элементе источника тока равно его ЭДС.

Согласно основным законам электротехники компонентные уравнения этих типовых элементов соответственно имеют вид

I= U /R; I= СdU/dt; U=LdI/dt.

Уравнения равновесия (первый закон Кирхгофа) и непрерывности (второй закон Кирхгофа), устанавливающие равенство нулю суммы токов в узлах схемы и суммы напряжений на элементах схемы при их обходе по произвольному контуру, дают топологические уравнения подсистемы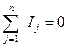

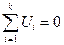
где п — число ветвей в узле схемы; к — число элементов в контуре схемы.

Механические поступательная и вращательная подсистемы. Типовыми элементами этих подсистем являются элементы трения, элементы массы и упругие элементы. В качестве фазовых переменных выступают сила F и скорость v для поступательной подсисте­мы и момент М и угловая скорость ω — для вращательной.

Математические модели элементов трения получаются из уравнений вязкого трения:

F =μv_от =v_оТ/(1/μ); М= kω_от = ω_от/(1/к),

где μ и к— коэффициенты диссипации соответственно для посту­пательной и вращательной подсистем; v_от,ω _от — относительные скорости контактируемых тел.

Введем понятия механического сопротивления при поступательном движении R_м = 1/μ и вращательной R_вр = 1/ к.

Тогда

F=v_от/R_m, M= ω_от/R_вр

Математическую модель массы выражает второй закон Ньютона:

F=mdv/dt M=Jdω/dt

где т — масса элемента; J — момент инерции массы относительно ее оси вращения.

Математическая модель упругого элемента получается из закона Гука. Для поступательной подсистемы

σ=E∆ l/l

где σ и ∆ — соответственно напряжение и удлинение стержня в продольном направлении; Е — модуль упругости первого рода; l — начальная длина стержня.

Так как σ = F/S, где S — площадь поперечного сечения стерж­ня, после дифференцирования по времени получим

dF/dt=SEv_om/ l =cv_om или v_om=(1/c)(dF/dt)=L_мdF/dt

где с — жесткость; v _ОТ = d l/dt — скорость деформации; L_м = 1/с — податливость.

Для вращательной системы при закрутке вала на угол φ получаем аналогичное компонентное уравнение

ωo_Т = (1/c_φ)(dM/dt) =L_MdF/dt

где с_φ — крутильная жесткость; ω_от = dφ /dt — угловая скорость деформации; L_вр = 1/с_ф — крутильная податливость.

Топологические уравнения подсистемы получаются из уравне-ний равновесия (принцип Д'Аламбера) и уравнений непрерывности (сумма абсолютной, переносной и относительной скоростей равна нулю):

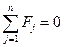
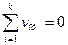
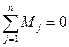
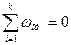
Особенностью механической поступательной системы является то, что в топологических уравнениях фигурируют не алгебраические, а геометрические суммы. Другими словами, топологические уравнения в виде алгебраических сумм должны записываться для проекций сил и скоростей на каждую ось координат.

Гидравлическая и пневматическая подсистемы. Основными фазовыми переменными этих подсистем являются массовый расход Q_т и давление р.

Рассмотрим компонентные уравнения гидравлической подси­стемы для участка трубопровода длиной l и диаметром d.

Потери давления ∆ р = р₁ - р₂ (р₁ р₂ — давление на начальном и конечном участках трубопровода соответственно) при стационарном ламинарном течении жидкости с кинематической вязкостью V могут быть определены по формуле Пуазейля

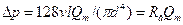
где Rг = 128v l/(πd⁴) — гидравлическое сопротивление.

Любая полость в гидравлической подсистеме может рассматриваться как емкость. Если полость заполнена жидкостью, компонентное уравнение гидравлической системы получается из обобщенного закона Гука:

Qm=C_гdp/dt

где С_г — приведенная гидравлическая емкость, С_г = V р/Е_ж; V — объем емкости; Е_ж — модуль упругости жидкости.

Инерционные свойства жидкости позволяет учесть одномерное уравнение Эйлера (закон движения идеальной жидкости):

dv/dt=-(1/p)(δp/ l)

где v — скорость течения жидкости; 8р = р₂ – p₁ — изменение давления на участке трубопровода длиной l, обусловленное инерционными свойствами жидкости.

Умножив обе части уравнения на рS и заменив δ р на ∆ р, получим

dQ_т/dt=(S/ l)∆p или ∆p=(l/S)(dQ_m/dt)=L_гdQ_m/dt

где Lг = l/S — гидравлическая индуктивность.

Топологические уравнения гидравлической подсистемы выво-дятся на основе законов, утверждающих, что сумма потоков в любой общей точке системы и сумма перепадов давления на замк-нутом контуре равны нулю:

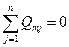
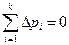
Для пневматической подсистемы все уравнения имеют анало-гичный вид, разница будет заключаться только в значениях коэф-фициентов.

Тепловая подсистема. Компонентные и топологические уравне­ния для тепловой подсистемы идентичны по форме уравнениям рассмотренных подсистем за исключением того, что в тепловой подсистеме присутствуют только два типа основных элементов: элементы теплопроводности и теплоемкости. Фазовыми переменными являются температура Т и тепловой поток Ф = dQ/dt, где Q — количество теплоты.

При выделении элементов твердое тело разбивается на участки, каждый из которых характеризуется средней теплоемкостью С_т. По определению

C_т = dQ/dT

следовательно:

dQ/dt = C _тdT/dt или ф = C_т dT/dt.

Кроме того, каждый участок обладает теплопроводностью. Математическая модель теплового сопротивления получается из урав­нения Фурье

q=-λ grad T,

где q — плотность теплового потока; λ — коэффициент теплопро­водности; Т — температура.

Если рассматривать передачу теплоты вдоль участка однородного тела с площадью поперечного сечения S и длиной l, то

Ф = λS(T₁-T₂)/ l =(T₁-T₂)/R_т=∆T/R_т

где R_Т = l /(λS) — тепловое сопротивление; ∆ Т = Т₁ - Т₂ — разность температур на границах элемента.

Для участков контакта твердого тела с жидкой или газообразной средой тепловое сопротивление определяеТся теплопередачей конвекцией. Компонентное уравнение элемента сопротивле­ния имеет в данном случае аналогичный вид, но R_Т = l /(Sα), где S — площадь контакта; α — коэффициент теплопередачи.

Топологические уравнения для тепловых подсистем следуют из уравнения теплового баланса для стационарного процесса тепло­передачи и закона, устанавливающего, что сумма изменений тем-пературы при обходе по замкнутому контуру равна нулю:

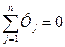
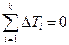
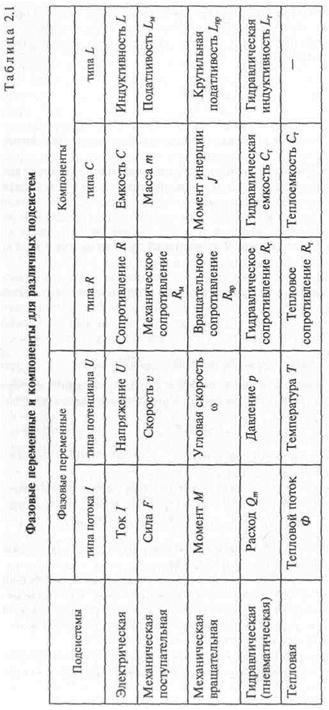
В уравнениях рассмотренных подсистем используются фазовые переменные двух типов: типа потока и типа потенциала — и ком­поненты трех типов: типа сопротивления К, типа емкости С и типа индуктивности Ь (у тепловой подсистемы компонент типа индуктивности Ь отсутствует). Нетрудно убедиться, что при пра-вильном выборе аналогий (табл. 2.1) для описания всех рассмот­ренных подсистем можно использовать идентичные уравнения. Данное обстоятельство дает возможность автоматизировать про­цесс получения ММ объектов после выполнения предваритель-ных процедур, связанных с получением формального представле-ния структуры этих объектов.

2.4. Формальное представление структуры объөкта на макроуровне

Для формального представления структуры объекта удобно использовать графические изображения, облегчающие пользова-телю восприятие модели и приводящие к представлению модели в той или иной схемной форме. Топологические уравнения сис-тем, представленных выше, записывались применителъно к уз-лам и контурам. Следовательне, сама форма топологических урав-нений требует отоҗцествления участков реальной структуры объек­тов или характеризующих әти участки величин с некоторыми вет-вями и узлами, поэтому первым этапом моделирования объектов должна быть замена реального объекта некоторым графическим представлением, состоящим из связанных между собой ветвей, — графами и эквивалентными схемами.

Графы применяются не только для представления топологи­ческих уравнений в моделях макроуровня. Ими широко пользуют-ся для получения структурных и функциональных математичес-ких моделей на разных уровнях проектирования, а также при ре-шении задач синтеза структуры.

Графом называют совокупность вершин (узлов) и связываю-щих их ребер (ветвей). Если для ребер графа указываются опреде-ленные направления, такой граф является направленным. Любая последовательность ребер, в которой соседние ребра инцидентны одной и той же вершине, называется маршрутом. Термин «инци-дентность» означает соотношение объектов типа «проходит че-рез...» или «находится на...».

Если в маршруте нет повторяющихся ребер, маршрут называ­ют цепью. Если цепь начинается и заканчивается в одной и той же вершине, имеем цикл.

Связным графом называют граф, в котором можно указать мар­шрут, связывающий любые вершины. Частным случаем связного графа без циклов является дерево. Его ребра называют ветвями.

Граф — удобное средство отображения структуры проектируе-мого объекта. Чаще всего при таком отображении вершины графа отоҗдествляются с элементами структуры, а ребра соответствуют связям между элементами. При моделировании объектов, наобо-рот, ребрами изображают элементы, а вершинами — связи между элементами.

Если граф отображает только такие структурные особенности, как способ связи элементов друг с другом, то эквивалентная схе­ма содержит более полную информацию об объекте, отображает физическую сущность отдельных элементов. Рассмотрим особен­ности представления моделей в виде эквивалентных схем.

В разных областях техники применяют специфические системы обозначений элементов на эквивалентных схемах. Будем исполь-зовать в дальнейшем единую систему обозначений для элементов всех подсистем, обычно применяемую при изображении электри-ческих эквивалентных схем, а при составлении схем придержи-ваться правил, приведенных ниже.

1.Эквивалентная схема, как и граф, состоит из множества вет-вей и множества узлов.

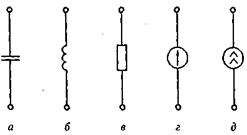
2.Каҗдая ветвь относится к одному из пяти возможных типов, изображенных на рис. 2.4.

3. Каждой ветви соответствует свое компонентное уравнение:
для емкостной (рис. 2.4, а) I = СdU/dt;

для иңдуктивной (рис. 2.4, б)U=LdI/dt;

для резистивной (рис. 2.4, в) I=U/R;

для ветви источника типа потенциала (рис. 2.4, г) уравнение, связывающее разность потенциалов U на узлах данной ветви с независимой переменной ( и, возможно (для зависимой ветви), с фазовыми переменными других ветвей: U =f₁(V,t), где V — вектор фазовых переменных; t— время. В частном случае U =const;

Рис.2.4. Типы ветвей в эквивалентных схемах

а-емкостная, б-индуктивная, в-резистивная, г- источника типа потенциала, д-источника типа тока.

для ветви источника типа потока (рис. 2.4, д) уравнение, связывающее поток I в данной ветви со временем t и, возможно (для зависимой ветви), с фазовыми переменными других ветвей: I=f₂(V,t). В частном случае I= соnst.

4. Каждому узлу схемы соответствует определенное значение фазовой переменной типа потенциала, а каждой ветви — значения переменных I и U, фигурирующих в компонентных уравнениях. Соединение ветвей друг с другом, т.е. образование узлов, должно отражать взаимодействие элементов в системе. Выполнение этого условия обеспечивает справедливость топологических уравнений для узлов и контуров схемы.

Зависимая ввтвъ — ветвь, параметр которой (U в источнике типа потенциала, I в источнике типа потока или R, С,L) зависит от каких-либо фазовых переменных.

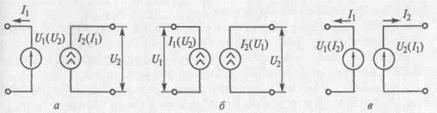
Для отражения взаимосвязей подсистем в их эквивалентные схемы вводят специальные преобразовательные элементы. Различают три вида связей подсистем. Трансформаторная и гираторная связи выражают соотношения между фазовыми переменными двух подсистем. Этим типам связей соответствуют элементы, представляемые парами источников тока или напряжения. Их называют зависимыми источниками. Третий вид связи выражает влияние фазовых переменных одной подсистемы на параметры элементов другой и задается в виде зависимостей С, L или R от фазовых переменных. Примеры изображения связей в эквивалентных схе-мах приведены на рис. 2.5. Здесь запись вида А(В) означает, что фазовая переменная А является функцией фазовой переменной В.

Таким образом, если нужно отобразить только топологические уравнения, достаточно использования графов; если нужно ото­бразить топологические и компонентные уравнения, целесооб-разно воспользоваться эквивалентными схемами. Следует, одна-ко, отметить, что, если эквивалентные схемы строить по приве-денным выше правилам, между ними и графами в отношении структуры имеется строгое соответствие. Тогда можно проставить у ветвей графа условные

Рис. 2.5. Примеры изображения связей в эквивалентных системах

а-трансформаторной, б,в-гираторной.

буквенные обозначения типов ветвей. В этом случае граф содержит ту же информацию, что и эквивалентная схема, и можно с равным успехом использовать оба графических представления объекта.

Рассмотрим общие правила составления эквивалентной схемы на примере механической системы. Сначала выбирается инерци-альная система отсчета, с которой связывается система коорди­нат (обычно декартова). После этого разрабатывается структурная схема, отражающая состав объекта и связи его элементов. Схема должна содержать все элементы, свойства которых предполагается учитывать в рамках поставленной задачи. На схеме наносятся источники внешних силовых и кинематических воздействий в виде сил (моментов) и скоростей. Инерционные элементы представ-ляются в виде сосредоточенных масс. Элементы, отражающие уп-ругие и демпфирующие свойства и внешние воздействия, часто ориентируются относительно осей координат. Назначаются обоб-щенные координаты системы — взаимно-однозначные функции ко­ординат, определяющие положение объекта в пространстве в каж-дый момент времени. Число обобщенных координат равно числу степеней свободы. Обобщенные координаты фигурируют в даль-нейшем в компонентных и топологических уравнениях: фазовые переменные типа потока являются функциями производных по времени от обобщенных координат (функциями обобщенных ско­ростей).

На основании структурной схемы строится эквивалентная схема:

• задается базовый узел, который в дальнейшем интерпретиру-ется как инерциальная система отсчета. В приведенных ниже при-мерах он обозначен номером 0;

• для каждого тела с учитываемыми инерционными свойства-ми в эквивалентной схеме выделяется отдельный узел. Если тело имеет несколько степеней свободы относительно осей коорди­нат, каждой из них должен соответствовать свой узел тела. Узел тела в дальнейшем интерпретируется как само тело, совершаю-щее движение относительно соответствующей оси координат: к узлу прикладываются силы (моменты), действующие на тело в выбранном направлении, потенциал узла характеризует скорость тела в этом направлении относительно инерциальной системы ко­ординат (обобщенную скорость);

• между узлом тела и базовым узлом включается емкостная ветвь; она характеризует силу (момент) инерции;

• трение между контактируемыми телами отражаются резис-тивной ветвью, включенной между их узлами;

• упругие элементы, соединяющие тела, отражаются индук-тивной ветвью между соответствующими узлами схемы;

• внешние силы (моменты) и внешние источники скорости, действующие на систему, учитываются в схеме соответственно ветвями источника типа потока и источника типа потенциала,включенными между базовым узлом и узлом элемента, к которо-му они приложены;

• узлы схемы нумеруются в произвольном порядке, начиная с 1.

В ряде случаев невозможно непосредственно связать все ветви схемы подобным образом. Наличие в системе преобразователей скорости и силы (момента), таких, например, как рычажные ме­ханизмы или зубчатые передачи, приводит к тому, что фазовые переменные контактируемых элементов требуют дополнительного согласования. То же самое может возникнуть, когда тело совершает одновременно поступательное и вращательное движения. В по-добных случаях при построении эквивалентной схемы использу-ются схемы, разработанные для отдельных подсистем и объеди-ненные между собой с помощью трансформаторных связей. Если в системе не учитываются упругие свойства связи между контак-тируемыми телами, в одну из подсистем между базовым узлом и узлом тела помещают зависимый источник типа потока, а в дру-гую — зависимый источник типа потенциала. При этом безраз-лично, какой из источников в какую подсистему будет включен. Если в системе присутствуют элементы податливости между контактируемыми телами, их характеристики должны быть при-ведены к фазовой переменной типа потока одной из связываемых подсистем, а сами они должны быть включены в эту подсистему посредством ветвей, один конец которых подсоединен к узлу тела. Между другим концом ветвей и базовым узлом помещают зави­симый источник типа потенциала. Зависимый источник типа по­тока размещают между узлом тела и базовым узлом другой подси-стемы.

Следует отметить, что скорости и силы (моменты) — это векторы, и поэтому при размещении в схеме их источников сле­дует правильно указывать их на-правление.

Более подробно правила составления эквивалентных схем с зависимыми источниками будут рассмотрены в примерах.

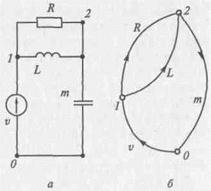
На рис. 2.6 изображены эквивалентная схема и соответствующий ей граф для ранее рассмотренного примера одномассовой колебательной системы, структурная схема которой приведена на рис. 2.3. Начало ко­ординат 0 здесь связано с инерциальной системой отсчета, совершающей движение в гори-

Рис.2.6. Эквивалентная схема (а) и граф (б) одномассовой колебательной системы.

зонтальной плоскости совместно с корпусом транспортного сред-ства. Система имеет одну степень свободы: рассматривается движение сиденья водителя в вертикальном направлении. В качестве обобщенной координаты выбрано вертикальное перемещение центра масс водителя и сиденья. Инерционные свойства водите­ля и сиденья учтены емкостной ветвью т, включенной между узлами О и 2. Потенциал узла 2 характеризует вертикальную скорость сиденья, а поток в емкостной ветви — силу инерции. Упругие и демпфирующие свойства подвески сиденья отражены в схеме ветвями L и R. Разность потенциалов в узлах 1 и 2 соответствует скорости деформации элементов подвески, а потоки в ветвях — действующим в них силам. Согласно условию задачи, колебания водителя на сиденье совершаются вследствие вертикального пе-ремещения корпуса, что отражено в схеме введением ветви у источника типа потенциала (источника кинематических воздей-ствий). Изменение потенциала в узле 1 характеризует изменение вертикальной скорости корпуса. Закон этого изменения должен быть задан в характеристике источника кинематических воздействий.

Дата добавления: 2014-01-03