Математика в 17 веке

В XVII в. начинается новый период истории математики — период математики переменных величин. Его возникновение связано прежде всего с успехами астрономии и механики.

И. Кеплер в 1609—1619гг. открыл и математически сформулировал законы движения планет. Г. Галилей к 1638 г. создал механику свободного падения тел, основал теорию упругости, применил математические методы для изучения движения, для отыскания закономерностей между путем движения, его скоростью и ускорением. И.Ньютон к 1686г. сформулировал закон всемирного тяготения.

Успехи естествознания (больше всего в механике и оптике^*) привели к необходимости создания математического аппарата для изучения процессов движения. Ученые XVII в. были одновременно математиками, естествоиспытателями, механиками. Нужно также отметить, что важнейшие открытия века, принадлежащие P. Декарту, И. Ньютону, Г. Лейбницу, неразрывно связаны с общей системой философских взглядов этих ученых.

^*Актуальные задачи ставились перед математикой 17 века также картографией, баллистикой, гидравликой.

*Математические достижения 17 в. начинаются открытием логарифмов. Шотландский математик Дж. Непер, опубликовавший свои таблицы в 1614 г., обосновывает их построение не ссылкой на давно известные свойства арифметических и геометрических прогрессий, а рассматривает непрерывное «течение» логарифма при изменении числа, т. е. впервые вводит представление о непрерывной функции, не заданной никаким алгебраическим выражением или геометрическим построением.

Первым решительным шагом в создании математики переменных величин было появление в 1637 г. книги Р. Декарта «Геометрия», в которой заложены основы метода координат и введена общая идея переменной величины. (*содержащую основы координатного метода в геометрии, классификацию кривых с подразделением их на алгебраические и трансцендентные)

Исследования Р. Декарта были вызваны насущными потребностями науки и техники. К этому времени И. Кеплер показал, что планеты движутся вокруг Солнца по эллипсам, Г. Галилей установил, что брошенное в сторону тело падает по параболе. Изучение конических сечений стало необходимостью.

Для развития астрономии необходимо было также вычислять криволинейные площади, ограниченные дугами эллипса, так как, согласно законам Кеплера, радиусы-векторы планет «заметают» за равные промежутки времени равные площади. И.Кеплер в 1615г. разработал метод вычисления площадей криволинейных фигур, каждую из которых он представлял состоящей из множества бесконечно малых частей. Например, по И. Кеплеру, круг состоит из бесконечно большого числа бесконечно узких секторов, каждый из которых можно рассматривать как равнобедренный треугольник. Так был создан интеграционный метод для вычисления криволинейных площадей и объемов, основанный на представлении о бесконечно малых.

Изучение законов механики также требовало создания новых математических методов. Ученик Г. Галилея Б. Кавальери разработал интеграционный метод, основанный на представлении о неделимых. Он считал, что точка (неделимая) при движении порождает линию, а линия — плоскость. При изучении объемов геометрических тел неделимыми являются плоскости. Метод Кавальери позволил ему решать задачи, равносильные отысканию определенных интегралов от многочленов.

К 60-м гг. XVII в. были разработаны многочисленные методы для вычисления площадей, ограниченных различными кривыми линиями: алгебраическими и тригонометрическими. Нужен был только один толчок — рассмотрение всей совокупности методов с единой точки зрения, чтобы из разрозненных приемов создать единое интегральное исчисление.

Так же обстояло дело и с развитием дифференциальных методов. В механике для изучения неравномерного движения было введено понятие мгновенной скорости, что привело в свою очередь к задачам на проведение касательных к кривым. Для решения этих задач в школе Г. Галилея применялись кинематические методы. Значительные успехи в этом направлении принадлежат П. Ферма. * Исследования французского математика П. Ферма о максимумах и минимумах и разыскании касательных к кривым уже содержат в себе, по существу, приемы дифференциального исчисления, но самые эти приемы еще не выделены и не развиты, и слова «производная» или «дифференциал» остаются еще не произнесенными

Дифференциальные методы решали основную задачу: зная кривую линию, найти ее касательные. Многие задачи практики приводили к постановке обратной задачи: зная касательные к кривой, найти соответствующую кривую. В процессе решения обратной задачи выяснилось, что к ней применимы интеграционные методы. Так была установлена глубокая связь между дифференциальными и интеграционными методами, что создало основу для возникновения единого исчисления.

Наиболее ранней формой дифференциального и интегрального исчисления является теория флюксий, построенная И. Ньютоном (1670-1671). Почти одновременно математический анализ был создан Г. Лейбницем (1673) в виде исчисления дифференциалов.

И. Ньютон изучал переменные величины, возникающие в результате непрерывного механического движения. Он называл их флюентами, т. е. текущими. По И. Ньютону, все флюенты зависят от времени. Затем он ввел скорости течения флюент, т. е. производные по времени, которые назвал флюксиями. Теория И. Ньютона основана на изучении движения.

Г. Лейбниц, так же как и И. Ньютон, открыл взаимообратную связь между методами проведения касательных и отыскания криволинейных площадей. Его символика оказалась очень удобной. Г. Лейбницем введены в науку термины дифференциал, функция, координаты, алгоритм. Оперативная простота исчисления Г. Лейбница привлекла внимание ученых.

^*Ньютон и Лейбниц впервые общем виде рассмотрели основные для нового исчисления операции дифференцирования и интегрирования функций, установили связь между этими операциями (т. н. формула Ньютона — Лейбница) и разработали для них общий единообразный алгоритм. Подход к делу у Ньютона и Лейбница, однако, различен. Для Ньютона исходными понятиями являются понятия «флюенты» (переменной величины) и ее «флюксии» (скорости ее изменения). Прямой задаче нахождения флюксий и соотношений между флюксиями по заданным флюентам (дифференцирование и составление дифференциальных уравнений) Ньютон противопоставлял обратную задачу нахождения флюент по заданным соотношениям между флюксиями, т.е. сразу общую задачу интегрирования дифференциальных уравнений; задача нахождения первообразной появляется здесь как частный случай интегрирования дифференциального уравнения 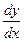= f(x)_. Такая точка зрения была вполне естественна для Ньютона, как создателя математического естествознания: его исчисление флюксий являлось просто отражением той идеи, что элементарные законы природы выражаются дифференциальными уравнениями, а предсказание хода описываемых этими уравнениями процессов требует их интегрирования. Для Лейбница в центре внимания находился вопрос о переходе от алгебры конечного к алгебре бесконечно малых; интеграл воспринимался прежде всего как сумма бесконечно большого числа бесконечно малых, а основным понятием дифференциального исчисления являлись дифференциалы — бесконечно малые приращения переменных величин (наоборот, Ньютон, вводя соответствующее понятие «момента», стремился в более поздних работах от него освободиться). С публикации работ Лейбница в континентальной Европе начался период интенсивной коллективной работы над дифференциальным и интегральным исчислением, интегрированием дифференциальных уравнений и геометрическими приложениями анализа, в которой принимали участие, кроме самого Лейбница, Я. Бернулли, И. Бернулли, французский математик Г. Лотшталь и др. Здесь создается современный стиль математической работы, при котором полученные результаты немедленно публи куются в журнальных статьях и уже очень скоро после опубликования используются в исследованиях других ученых.

Кроме аналитической геометрии, развивается в тесной связи с алгеброй и анализом дифференциальная геометрия (в области последней следует отметить, в частности, введение понятия радиуса кривизны у Кеплера (1604), изучение эволют и эвольвент у Гюйгенса (1673) и т. п.), в 17 в. закладываются основы дальнейшего развития чистой геометрии, главным образом в направлении создания основных понятий проективной геометрии. Французский математик Ж. Дезарг, занимаясь теорией перспективы (1636), развил целую систему представлений о бесконечно удаленных элементах, ввел понятие инволюции и т. д. Теория конических сечений разрабатывается с проективной точки зрения французскими математиками Ж. Дезаргом (1639), Б. Паскалем (1640), Ф. Лагиром (1685). Из других открытий 17 в. следует отметить: в теории чисел — формулировку принципа математической индукции (Б. Паскаль, 1665) и глубокие исследования П. Ферма, в значительной мере определившие дальнейшее развитие этой науки; разработку основных понятий комбинаторики (П. Ферма, Б. Паскаль, Г. Лейбниц); первые работы по теории вероятностей (П. Ферма, Б. Паскаль), увенчавшиеся в конце века результатом принципиального значения — открытием простейшей формы закона больших чисел (Я. Бернулли, опубликовано в 1713); теорию непрерывных дробей [итальянский математик П. Катальди (1613), немецкий математик Д. Швентер (1617, 1618), Дж. Валлис (1656), X. Гюйгенс (1703)]; метод неопределенных коэффициентов (Р. Декарт, 1637); формулировку так называемой теоремы Эйлера о многогранниках (Р. Декарт, ок. 1620). Необходимо указать еще на построение Б. Паскалем (1641) и Г. Лейбницем (1673—74) первых счетных машин, оставшееся надолго, впрочем, без практических последствий.

Создание исчисления бесконечно малых в XVII в. было основано на глубоких общих идеях, что сближало математику с философией. Г. Лейбниц исходил из философской цели отыскания универсального метода научного познания. Он стремился к разработке общего логико-математического аппарата суждений. Для И. Ньютона, крупнейшего естествоиспытателя, математика представляла собой часть общей науки о природе — натуральной философии. Он разрабатывал общий метод, основанный на изучении непрерывного движения и связанных с ним понятий скорости и ускорения.

Развитие математики в XVIII в.

XVIII век характеризуется решительной победой в Европе капиталистического способа производства. Решение научно-технических задач становится делом общегосударственной важности, и математика в этот период оказывается необходимой для развития промышленности, военной техники, кораблестроения, составления географических карт.

* Математики 18 в.—это люди из разных кругов общества, рано выделившиеся свои­ми математическими способностями, с быстро развивающейся академической карьерой (Эйлер, происходя из пасторской семьи в Базеле, в возрасте 20 лет был приглашен адъюнктом в Петербургскую академию наук, 23 лет становится там же профессором, 37 лет — председателем физико-математического класса Берлинской академии наук; Лагранж — сын французского офицера, 18 лет — профессор в Турине, 30 лет — председатель физико-математического класса Берлинской академии наук; Лаплас — сын французского крестьянина, 18 лет -— преподаватель математики в военной школе в Бомоне, 20 лет — профессор военной школы в Париже, 37 лет — член Парижской академии наук).

Математики XVIII в. работали одновременно в области естествознания и техники. Л. Эйлер получил выдающиеся результаты в механике, занимался кораблестроением и оптикой. Ж. Лагранж создал основы аналитической механики. Его труд, появившийся через сто лет после работ И. Ньютона, показал, как много результатов можно получить в механике благодаря мощным методам математического анализа. Монументальное произведение П. Лапласа «Небесная механика» подвело итоги всех предшествующих работ в этой области.

XVII век дал математике мощный аппарат — анализ бесконечно малых. Новые идеи довольно быстро получили широкое распространение.

Важнейшим отличием созданного исчисления была глубокая систематичность его алгоритмов, удобная символика, сравнительно легкая выполнимость действий. Разработанные методы позволяли решать большое число новых задач. Так, если в древности для отыскания площади, ограниченной параболой, нужен был гений Архимеда, то теперь гораздо более сложные задачи стали доступны каждому, изучившему приемы интегрального исчисления. Результаты дифференциального и интегрального исчисления успешно использовались в науке и технике, и это заставляло ученых стремиться к новым достижениям. Для успешного продвижения вперед необходимо было в первую очередь усовершенствовать математический аппарат, обобщить существующие методы, разработать новые приемы, распространить их на более общие задачи.

В этот период Л. Эйлер ввел в математику символ f(x) для функции и показал, что функциональная зависимость является основным объектом изучения математического анализа. Были введены и изучены функции многих переменных. Соответственно обобщалась теория дифференцирования и интегрирования функций. Разрабатывались способы вычисле­ния частных производных, кратных и криволинейных интегралов, дифференциалов от функций многих переменных.

Основным инструментом в изучении функций стал аппарат их разложения в бесконечные степенные ряды. В XVIII в. были найдены степенные ряды для всех элементарных функций.

В математическом анализе систематически использовались комплексные числа, которые раньше появлялись в науке лишь эпизодически в связи с решением алгебраических уравнений. Было замечено, что корни алгебраических уравнений всегда имеют вид 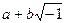, и введен символ i = 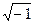. Сравнивая разложения функций в ряды, Л. Эйлер установил глубочайшую зависимость между показательной и тригонометрическими функциями е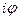= cos 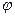+ i sin .

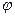В XVIII в. из математического анализа выделился ряд важных математических дисциплин, имеющих большое прикладное значение: теория дифференциальных уравнений, вариационное исчисление, теория функций комплексного переменного. Из геометрических приложений анализа выделилась дифференциальная геометрия. В XVIII в. началась разработка теории вероятностей.

Более подробно

Переходя к обзору достижений математики 18 века по отдельным областям, начнем с теории чисел. Благодаря работам Л. Эйлера, Ж. Лагранжа и французского математика А. Лежандра, теория чисел впервые приобретает характер систематической науки. Лагранж дал (1769г., опубликовано в 1771 г.) общее решение неопределенных уравнений второй степени. Эйлер установил (1772 г., опубликовано в 1783 г.) закон взаимности для квадратичных вычетов. Он же привлек (1737, 1748, 1749 гг.) для изучения простых чисел дзета-функцию, чем положил начало аналитической теории чисел.

При помощи разложений в непрерывные дроби Л.Эйлер доказал (1737 г.,опубликовано в 1744г.) иррацио­нальность е и е², а немецкий ученый М. Ламберт (1766 г., опубликовано в 1768 г.) — иррациональность 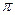. В алгебре швейцарский математик Г. Крамер (1750) ввел для решения систем линейных уравнений определители (известные ранее Лейбницу, не опубликовавшему своего открытия). Дальнейшей разработкой линейной алгебры занимались П. Лаплас и французский математик А. Вандермонд. И. Ньютон, Л. Эйлер и французский математик Э. Безу развивали теорию делимости многочленов и теорию исключения. Эйлер рассматривал как эмпирически установленный факт существование у каждого алгебраического уравнения корня вида 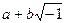. Д'Аламбер доказал (1748), что модуль многочлена не может иметь минимума, отличного от нуля (так называемая лемма Д'Аламбера), считая это за доказательство существования корня у любого алгебраического уравнения. Формулы английского математика А. Муавра и Л. Эйлера, связывающие показательную и тригонометрические функции комплексных аргументов, привели к дальнейшему расширению применений комплексных чисел в анализе. И. Ньютон, шотландский математик Дж. Стирлинг и Л. Эйлер заложили основы исчисления конечных разностей. Лагранж развивал символическое исчисление, рассматривая положительные и отрицательные степени операторов 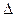и d; Лаплас дал общие методы решения разностных уравнений. Английский математик Б. Тейлор открыл (1715) свою формулу разложения произвольной функции в степенной ряд. У исследователей 18 в., особенно Эйлера, ряды становятся одним из самых мощных и гибких орудий анализа. С Д'Аламбера начинается серьезное изучение условий сходимости рядов. Эйлер, Лагранж и особенно Лежандр заложили основы исследования эллиптических интегралов — первого вида неэлементарных функций, подвергнутого глубокому специальному изучению. И. Бернулли, итальянский математик Дж. Риккати, Д. Бернулли, Л. Эйлер и французский математик А. Клеро интегрируют новые типы обыкновенных дифференциальных уравнений первого и второго порядка. Эйлер дал (1739 г., опубликовано в 1743 г.) первый метод решения линейного дифференциального уравнения любого порядка с постоянными коэффициентами. Д'Аламбер рассматривал системы дифференциальных уравнений. Лагранж и Лаплас развивали общую теорию линейных дифференциальных уравнений любого порядка. Эйлер, французский математик Г. Монж и Лагранж заложили основы общей теории дифференциальных уравнений с частными производными первого порядка, а Эйлер, Монж и Лаплас — второго порядка. Специальный интерес представляет уравнение колебания струны и связанное с ним введение в анализ разложения функций в тригонометрические ряды, так как в связи с этой задачей между Эйлером, Д. Бернулли, Д'Аламбером, Монжем и Лагранжем развернулась полемика по вопросу о понятии функции, подготовившая фундаментальные результаты 19 в. о соотношении между аналитическим выражением и произвольным заданием функции. Наконец, новым отделом анализа, возникшим в 18 в., является вариационное исчисление, созданное Эйлером и Лагранжем, А. Муавр, Я. Бернулли, П. Лаплас и английский математик Т. Байес на основе отдельных достижений 17—18 вв. заложили начала теории вероятностей.

В области геометрии Эйлер привел к завершению систему элементарной аналитической геометрии. Начиная с Ньютона, систематически изучаются кривые третьего порядка. Английский математик Э. Варинг установил ряд свойств алгебраических кривых любого порядка. В работах Эйлера, Клеро, Монжа и французского математика Ж. Менье были заложены основы дифференциальной геометрии пространственных кривых и поверхностей. Проблемы дифференциальной геометрии явились одним из основных источников упомянутого выше развития теории дифференциальных уравнений с частными производными. Ламберт развил теорию перспективы, а Монж придал окончательную форму начертательной геометрии.

Из приведенного обзора видно, что математика 18 века, основываясь на идеях 17 века, по размаху работы далеко превзошла предыдущие века. Этот расцвет математики был связан по преимуществу с деятельностью академий; университеты играли меньшую роль. Отдаленность крупнейших математиков от университетского преподавания возмещалась той энергией, с которой все они, начиная с Эйлера и Лагранжа, писали учебники и обширные, включающие отдельные исследования, трактаты. Новую струю в организацию науки внесла в конце 18 в. французская буржуазная революция. Крупнейшие ученые (Лагранж, Лаплас, Лежандр, Монж) привлекаются к созданию метрической системы мер, связанному с ней измерению меридиана, организованному на государственные средства вычислению новых тригонометрических таблиц и т. д. Наиболее важным для дальнейшего развития математики оказалось учреждение в 1794 г. Политехнической школы в Париже, возглавленной Монжем и сделавшейся для Франции в начале 19 в. основным рассадником математической культуры.

Проблемы обоснования математики переменных величин

Слабой стороной математики XVIII в. было отсутствие обоснования ее важнейших частей. Был развит аппарат анализа бесконечно малых без достаточной работы над его строгим логическим обоснованием.

Так, в интегральном исчислении для подсчета длин кривые линии заменялись многоугольниками. Аналогично при вычислении площадей криволинейные фигуры разбивали на бесконечно малые части, каждую из которых считали прямоугольной. При этом фактически отбрасывали бесконечно малые более высокого порядка, чем длины отрезков разбиения.

Корректность этой операции объяснялась различными путями. Так, Г. Лейбниц апеллирует к движению. Он пишет, что, строго говоря, покой не есть род движения, равенство не есть частный случай неравенства, равно как и круг не есть правильный многоугольник. Но можно сказать, что покой, равенство, круг ограничивают движения, неравенства и правильные многоугольники, которые приходят к первым, исчезая при непрерывном изменении. Понятие бесконечно малой величины оставалось невыясненным. И. Ньютон для его объяснения также прибегал к движению. Он говорил о величинах в момент их зарождения и в момент их исчезновения.

Теория неделимых Кавальери также вызывала серьезные возражения. Она была неприменима для вычисления длин кривых, так как неделимые точки безразмерны. Аналогичные логические трудности возникали, если площади представлялись линиями, не имеющими ширины. Само понятие неделимого было не выяснено.

В процессе обоснования понятия производной также остро вставал вопрос о существе бесконечно малой величины. Так, при вычислении производной от функции у = х² переменной х давали бесконечно малое приращение h. Затем приращение функции (х + h)² - х² делили на приращение аргумента h:

.

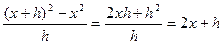Отбрасывая величину h, получали окончательный результат — производная от функции у = х² равна 2х.

Корректность отбрасывания бесконечно малой величины оставалась совершенно неясной. Если h = 0, то нет самого процесса перехода от х к соседней точке. Если h 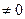, то h нельзя отбрасывать.

Этот период развития исчисления бесконечно малых называют мистическим. Исчисление существовало, давало много важных результатов, но логические основы его оставались невыясненными.

Была предложена теория компенсации ошибок: в методе бесконечно малых исчисление исправляет само допускаемые в нем ложные предположения. Когда, например, рассматривают кривую как многоугольник с бесконечным числом малых сторон, то явным образом делают ложное допущение. Но ошибка погашается при вычислении другой ошибкой, состоящей в пренебрежении как равными нулю количествами, предполагаемыми лишь бесконечно малыми.

В 1734 г. с критикой основ анализа выступил епископ Беркли. Он писал о том, что исчисление бесконечно малых ошибочно, ложно и приводит к цели лишь случайным образом. Критикуя теорию флюксий И. Ньютона, Д. Беркли писал: «Тот, кто может переварить вторую и третью флюксию, не может придираться к чему-нибудь в богословии».

В XVIII в. неясность основ стала тормозить развитие анализа. В математике накопилось большое число противоречий, парадоксов, возникающих прежде всего в теории бесконечных рядов, служивших основным орудием анализа. Так, при изучении ряда, являющегося геометрической прогрессией 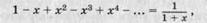полагали х=1. Из этого следовало равенство

1-1 + 1-1 + 1...=.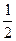

Если же члены ряда 1-1 + 1-1 + 1... сложить попарно, то в сумме получается нуль.

Это приводило к нелепости 1/2 = 0 и служило иногда для подкрепления теории о сотворении богом мира из ничего.

Накопившиеся противоречия явно показывали, что с бесконечными рядами нельзя обращаться как с конечными суммами. Вопросы бесконечного требовали строго логического обоснования.

В XVIII в. математики использовали много различных способов изложения анализа, но ни один из них не мог удовлетворительно объяснить его основы. Только по отношению к методам, основанным на понятии предельного перехода, критика не обнаружила логических пробелов. Сторонники теории пределов — Ж. Даламбер, С. Люилье, С. Е. Гурьев и другие — неустанно ее совершенствовали.

Решающие изменения произошли в первой половине XIX в., когда трудами О. Коши, Н. Абеля и других ученых исчисление бесконечно малых было обосновано на базе теории пределов. Было выяснено существо бесконечно малой величины. По О. Коши, это переменная величина, предел которой равен нулю. С помощью предела получили объяснение важнейшие понятия анализа: производная, интеграл, непрерывность функции, сумма ряда.

Нужно заметить, что понятие предела у О. Коши основано на представлениях, связанных с движением. Бесконечно малая у него — это движущаяся, бесконечно убывающая величина. Используя интуитивное представление о бесконечно малой текущей величине, О. Коши, однако, в ряде случаев пришел к неверным теоремам. Так, он доказал, что если функция многих переменных непрерывна по каждому переменному в отдельности, то она непрерывна по совокупности аргументов.

Однако вскоре был найден пример, опровергающий теорему О. Коши. Ошибка О. Коши объясняется использованием представлений о текущих бесконечно малых, отсутствием точных оценок. Чтобы избежать ошибок такого рода, потребовалось дальнейшее уточнение понятий предела и бесконечно малой. Оно было проведено К. Вейерштрассом в 70-х гг. XIX в.

По К. Вейерштрассу, бесконечно малую нельзя рассматривать просто текущей во времени, а необходимо указывать каждый раз, в каком процессе происходит изменение переменной. Так, например, а_п = 1/п² — бесконечно малая последовательность в процессе неограниченного увеличения номера п. Функция у = sin x является бесконечно малой в процессе неограниченного уменьшения аргумента х. Для получения строгих определений К. Вейерштрасс разработал систему 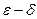неравенств. Эта уточненная теория пределов лежит в основе современного изложения основ математического анализа.

Таким образом, современный анализ заменил использование интуитивных представлений, связанных с движением, строгим математическим аппаратом неравенств, и так как все вопросы были сведены к неравенствам с числами, то перед математикой встала новая проблема — уточнить понятие действительного числа.

В теории пределов, как известно, ряд теорем основан на утверждении: если переменная величина возрастает и ограничена, то она имеет предел. Интуитивно ясное, это утверждение потребовало для своего доказательства построения теории действительного числа.

Такие теории появились. Почти одновременно в 1872 г. были построены теории действительного числа Г. Кантором, К. Вейерштрассом и Р. Дедекиндом. Различные по форме, эти теории выясняли одну и ту же проблему — существо непрерывности числовой прямой.

Р. Дедекинд пишет по этому поводу: «Мы приписываем прямой полноту, отсутствие пробелов, непрерывность. В чем же собственно состоит эта непрерывность? Все заключается в ответе на этот вопрос, и только в этом ответе мы приобретаем научное основание для исследования всех непрерывных областей. Смутными разговорами о непрерывной связи малейших частиц, конечно, ничего не достигнешь».

Изучение действительных чисел, в свою очередь, привело математику к рассмотрению бесконечных множеств. Как показала теория множеств, развитая в конце XIX в. Г. Кантором, Р. Дедекиндом и др., множество действительных чисел не является счетным. В процессе развития теории множеств в ней выявились парадоксы, противоречия, связанные в особенности со свойствами несчетных множеств.

Дата добавления: 2014-01-03