Поиск оптимальной области

Решение различных задач управления, проектирования и планирования в той или иной мере связано с оптимизацией, нахождением наилучших в определенном смысле различных параметров (факторов). Задача оптимизации может быть решена путем исследования математической зависимости, описывающей область факторного пространства в широком интервале изменения факторов. Однако такие зависимости часто очень сложны. Обычно исследователи идут другим путем: сначала находят оптимальную область, а затем описывают ее уравнением второго или третьего порядка. В настоящее время существует много различных методов поиска оптимальной области, которые можно разбить на две группы: детерминированные и статические.

В детерминированных методах движение к оптимальному осуществляется на основе информации, получаемой от пробных движений, совершаемых в определенной последовательности.

В статистических методах пробные движения производятся случайным образом, а движение к оптимуму является вполне определенным следствием реакций на случайные пробы.

В практике ПЭ наиболее широко применяются детерминированные методы поиска. Рассмотрим некоторые из них.

Метод Гаусса – Зейделя (метод покоординатного подъема).

Здесь все факторы, кроме одного, поочередно фиксируются (схема однофакторного эксперимента): исследователь изучает поведение каждого фактора в отдельности. Ставится серия опытов при различных значениях фактора и, таким образом, двигаясь параллельно одной из осей факторного пространства, находится наилучшее для рассматриваемого разреза поверхности отклика значение параметра оптимизации. Затем ставится серия опытов для следующего фактора. Последовательное прохождение всех осей факторного пространства составляет первый цикл исследования. Затем процедуру повторяют до получения оптимума или до попадания в некоторую точку, любое движение из которой «ухудшает» значение параметра оптимизации.

Распространенным недостатком при использовании данного метода является прекращение работы после выполнения первого цикла. Данный метод требует большого количества опытов.

Метод крутого восхождения (метод Бокса – Уилсона).

Последовательный — «шаговый» метод изучения поверхности.

Сначала ставится небольшая серия опытов (дробный ФЭ) для локального описания небольшого участка поверхности отклика полином первого порядка. Далее движение осуществляется по поверхности отклика в направлении градиента линейного приближения. Это движение сопровождается одновременным изменением всех факторов. Если одного линейного приближения оказывается недостаточно, то ставится новая небольшая серия опытов и находится новое направление для движения по поверхности отклика. Такой шаговый процесс продолжается до тех пор, пока исследователь не попадет в «почти стационарную область», где линейное приближение уже недостаточно. Здесь ставится большая серия опытов, и поверхность отклика описывается уже полиномом второго или третьего порядка. При таком подходе достигается высокая концентрация опытов в той части поверхности отклика, которая преимущественно и интересует исследователя.

Известно, что движение в направлении градиента — это движение по кратчайшему пути. Если поверхность отклика описана локально линейным уравнением, то частные производные равны коэффициентам регрессии. Для движения здесь независимые переменные необходимо изменять пропорционально величине соответствующих коэффициентов регрессии, с учетом их знака. Величина шага должна быть пропорциональна произведению 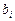на интервал изменения 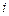-го фактора.

На рис. 3.3 приведено сравнение двух рассмотренных методов.

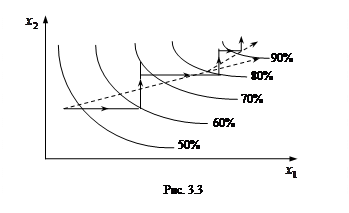Пунктирной линией показано движение методом крутого восхождения, а сплошной — методом покоординатного подъема. Из рисунка видно, что при использовании метода крутого восхождения путь, который необходимо найти экспериментатору, значительно сокращается. С возрастанием числа факторов эффект от применения метода крутого восхождения значительно повышается.

Практическое применение методов связано с принятием решений после построения линейной модели и после крутого восхождения.

Дата добавления: 2014-01-03