Пример 3.2

Предположим, что мы хотим оценить среднесуточный выход продукции химического завода так, чтобы оценка с вероятностью 0,95 лежала в пределах 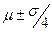. Тогда 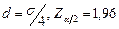и .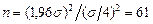

Если это возможно, следует определить дисперсию выхода с помощью пробного эксперимента и получить оценку 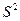дисперсии, а затем вычислить полное число необходимых наблюдений. Тогда

,

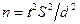где 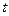— табулированная величина для заданного доверительного интервала и числа степеней свободы начальной выборки ;

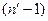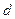— половина ширины доверительного интервала.

2. Оценивание дисперсии совокупности.

Построение доверительных интервалов часто требует оценивания среднеквадратического отклонения совокупности как меры дисперсии выборочных значений. Задачу оценивания дисперсии совокупности можно поставить как задачу отыскания оценки 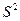такой, что

,

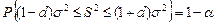где 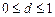— число, характеризующее степень близости оценки 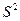к истинной дисперсии .

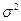Можно показать, что для достаточно больших 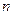(распределение 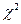можно аппроксимировать параллельным распределением)

.

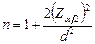3. Сравнение двух распределений.

Часто возникает задача проверки близости распределения отклика модели к некоторому другому распределению. Нас интересует объем выборки, при котором достигается желаемая точность сравнения распределений. Под желаемой точностью здесь будем понимать максимальную разность сравниваемых распределений во всех точках 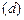. При заданном уровне значимости получим следующее уравнение:

,

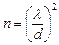где 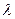— табличное значение функции Колмогорова.

Для разрешения третьей проблемы тактического планирования используются методы уменьшения дисперсии, которые позволяют при заданном объеме выборки увеличить точность оценок и наоборот. Эти методы используют информацию о структуре модели и свойствах ее входов.

Так как эти методы довольно громоздки, мы не будем рассматривать их подробно, а лишь перечислим некоторые из них: стратифицированные выборки; выборка по значимости; русская рулетка; метод коррелированных выборок; метод компенсации. Отметим, что интерес к этим методам начал падать с увеличением быстродействия ЭВМ, хотя применение этих методов в довольно простых искусственных задачах приводит к удивительным результатам.

Еще одним методом увеличения точности является метод, состоящий в задании доверительных интервалов для выходных величин и остановки прогона модели по достижении заданного доверительного интервала (четвертая проблема тактического планирования). Однако при введении в модель правил остановки и операций вычисления доверительных интервалов увеличивается машинное время, необходимое для получения одной выборочной точки. Кроме того, существует риск преждевременной остановки и получения оценок на основе слишком малой выборки.

Существует два основных способа включения в модель правил автоматической остановки:

1. Проводить прогон модели в два этапа. Сначала сделать прогон, позволяющий получить выборку объемом 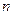, затем использовать полученную выборку для оценивания необходимого объема выборки 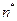. Если 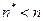, то следует закончить прогон, иначе продолжать до получения недостающих (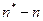) выборочных значений.

2. Использовать последовательную выборку для определения минимальной величины 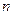, по которой можно с достаточной точностью определять среднеквадратическое отклонение 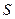, затем сравнивать величину 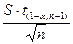с заданным уровнем 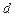и останавливать прогон в тот момент, когда эта величина становится меньше .

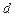Дата добавления: 2014-01-03