Вероятностно-статистические характеристики

Результаты измерений неизбежно содержат случайные погрешности, действие которых непредсказуемо. Поэтому результаты измерений рассматриваются как случайные величины с применением теории вероятностей.

Случайной величиной называют величину, которая в результате опыта принимает значение заранее неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. При проведении измерений внимание уделяется закономерностям случайных явлений, которые обладают относительной устойчивостью в их массовом проявлении. Случайное событие называется массовым, если может появиться в результате испытаний, которые могут быть повторены любое число раз при одних и тех же условиях. Случайные величины могут быть дискретными и непрерывными (аналоговыми). Возможные значения дискретных случайных величин отделимы друг от друга и поддаются счету. Возможные значения непрерывных случайных величин неотделимы друг от друга и непрерывно заполняют некоторый конечный или бесконечный интервал значений. Даже в любом конечном интервале непрерывная случайная величина имеет бесконечное множество значений.

Массовое случайное событие - результат многократных измерений - может быть охарактеризовано абсолютной частотой, относительной частотой, распределением вероятностей и функцией распределения вероятностей.

Абсолютная частота m_ί - число появлений одного и того же события (результата измерений).

Относительная частота 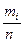- доля конкретного события (конкретного значения результата измерений) в общем числе событий (далее - результатов измерений). Относительная частота является показателем вероятности P_ί дискретного результата измерений:

P_ί=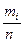 (3.1)

Распределение вероятностей представлено на рисунке 3.1.

Вероятность Pί
	Значение результатов измерений Qί

Рисунок 3.1 – Дискретное распределение вероятностей

Функция распределения вероятностей F(Q) является функцией накопленных относительных частот:

F(Q)=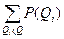 (3.2)

Дискретная функция распределения вероятности представлена на рисунке 3.2.

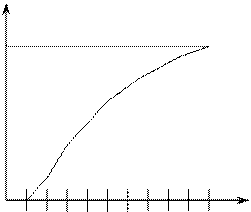
Результат измерений при непрерывном отсчете описывается плотностью вероятности р(Q_ί) текущего значения Q (рисунок 3.3, а) и функцией распределения вероятностей F(Q) (рисунок 3.3, б):

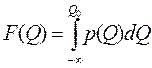(3.3)

Функция распределения вероятностей F(Qi)
	Значения результатов измерений Qi

Рисунок 3.2 – Дискретная функция распределения вероятностей F(Q_ί)

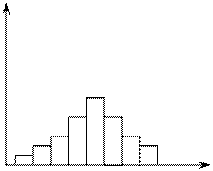Плотность вероятности P(Q)
	Результаты измерений Q б) Результаты измерений Q a)

Рисунок 3.3 – Эмпирические плотность вероятностей (а), функция распределения вероятностей (б)

Функция распределения вероятностей определяет вероятность того, что отдельный результат измерения Q при однократном измерении примет значение меньшее её аргумента. Чем больше результат измерения Q, тем больше вероятность того, что ни один результат измерений не превысит этого значения, т.е. F(Q) - неубывающая функция.

F(Q₂)≥F(Q₁), если Q₂>Q_1. При изменении Q от -∞ до +∞ F(Q) изменяется от 0 до 1.

Результат измерений Q меньше некоторого Q₁ c вероятностью F(Q₁) и меньше Q₂ с вероятностью F(Q₂). Причем Q₂>Q_1. Тогда вероятность того, что результат измерений окажется в интервале значений от Q₁ до Q₂:

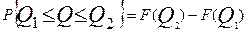(3.4)

или

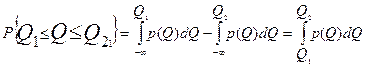(3.5)

При расширении интервала интегрирования до бесконечности рассматриваемое событие становится достоверным, поэтому площадь, ограниченная графиком функции распределения плотности вероятности для любого закона распределения и осью абсцисс, равна 1:

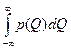=1 (3.6)

Дата добавления: 2014-01-03