Числовые (точечные) характеристики

Вероятностные характеристики результатов измерений являются наиболее полными, но не всегда удобны, а также не всегда достижимы, т.к. для их получения необходимо большое число экспериментальных данных. Поэтому чаще используют числовые характеристики через начальные и центральные моменты.

Начальные моменты получают усреднением значений относительно начала координат по правилу:

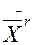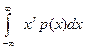=, (3.7)

где r – номер (порядок) момента;

х – случайная величина (результат измерений).

Первый начальный момент характеризует математическое ожидание отсчета при бесконечном повторении процедуры сравнения (измерения):

М(х)=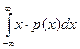 (3.8)

Для дискретных результатов измерений:

М(х)»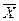= 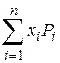(3.9)

где 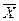- среднее арифметическое значение;

х_ί - ί-й результат измерений;

P_ί - вероятность появления ί-го результата;

n - число результатов измерений;

P_ί=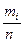 (3.10)

где m_ί - абсолютная частота ί-го результата.

Тогда

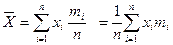(3.11)

М(х) так же как 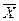характеризует центр группирования результатов многократных измерений.

Центральные моменты получают усреднением значений относительно центра распределения, т.е. относительно математического ожидания или среднего арифметического значения, по правилу:

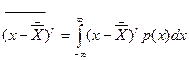(3.12)

Второй центральный момент называется дисперсией D(х) и характеризует разброс экспериментальных данных относительно центра распределения.

D(x)=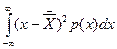 (3.13)

Для дискретных величин

D(x)=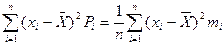 (3.14)

Часто в качестве характеристики разброса результатов измерений используется среднее квадратическое отклонение (СКО)- :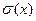

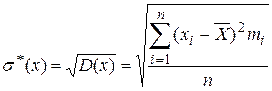(3.15)

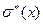-является смещенной оценкой СКО.

Если из общего числа данных при усреднении исключается одно значение, совпадающее с центром распределения, то такая оценка СКО является несмещенной:

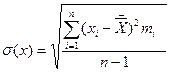(3.16)

Если каждый из результатов измерений встречается не более одного раза, то соответственно числовые характеристики определяются по формулам:

- среднее арифметическое значение:

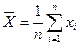; (3.17)

- СКО:

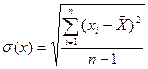(3.18)

Упрощенный расчет дисперсии можно выполнить по свойству дисперсии:

D(x)=M(x²)-M²(x) (3.19)

Третий центральный момент 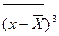используется для характеристики асимметричности кривой распределения плотности вероятности. Асимметрия определяется по формуле:

m=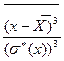 (3.20)

Четвертый центральный момент 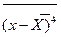используется для расчета эксцесса, характеризующего заостренность кривой распределения плотности вероятности:

ν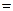 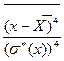(3.21)

Характеристики с использованием центральных моментов приведены на рисунке 3.4.

К числовым характеристикам также относятся мода и медиана. Модой М_о называется наиболее вероятное значение результата измерений. Мода соответствует абсциссе точки максимума кривой распределения плотности вероятности, как показано на рисунке 3.5.

Медиана М _l –это значение результата измерений, относительно которого равновероятно, что результат измерений окажется меньше или больше медианы:

Р(х < М _l)=Р(х > М _l)=0,5 (3.22)

На рисунке 3.5 медианой является значение абсциссы перпендикуляра к оси абсцисс, относительно которого площадь под кривой распределения плотности вероятности делится пополам.

Для симметричных распределений все три характеристики – математическое ожидание, мода и медиана - совпадают.

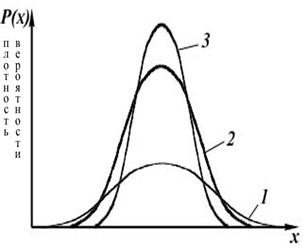
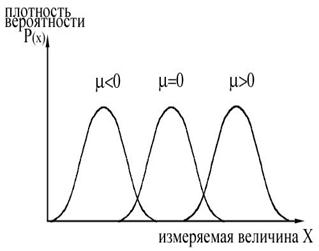
Рисунок 3.4 - Числовые характеристики результатов измерений

а).СКО и эксцесс; б).асимметрия

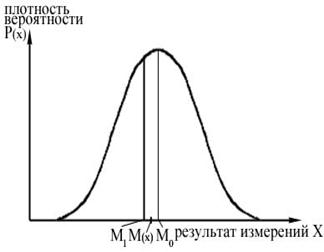
Рисунок 3.5 – Математическое ожидание, мода, медиана

Дата добавления: 2014-01-03