Основные положения

Ранее было сказано, что результат каждого отдельного измерения при наличии случайного рассеивания невозможно заранее предсказать. В то же время повторные измерения обнаруживают определённую закономерность, которая достаточно хорошо изучена и математически описывается кривой нормального распределения, показанной на рисунке 3.4 (кривая 2). Параметры этой кривой, наиболее полно характеризующие конечный результат измерений, приведены в главе 3.

Зная общую закономерность распределения данных, можно не только достаточно точно их описать, но и предсказать в целом течение и результат процесса. Достоверность таких выводов будет зависеть от правильности определения теоретического закона распределения, которому подчиняются экспериментальные данные.

Проверку гипотезы о виде эмпирического распределения можно выполнять по критериям Пирсона - c², Колмогорова – Смирнова, составному и другим.

Критерий Пирсона - c² применяется при большом числе экспериментальных данных n ³ 50. Параметром критерия является значение c², учитывающее расхождение эмпирической и теоретической абсолютных частот по интервалам гистограммы:

c² = 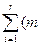_i – n×p_i)² /n×p_i, (7.1)

где r - число интервалов разбиения гистограммы;

m_i - абсолютная частота в i-том интервале;

p_i - теоретическая вероятность попадания в i-тый интервал;

n - общее число экспериментальных данных.

Гипотеза о соответствии нормальному распределению принимается, если выполняется условие:

c² < c_q², (7.2)

где c_q² - табличное значение по c²-распределению при уровне значимости q и числе степеней свободы f = r-3 (приложение e).

Составной критерий применяется при небольшом числе экспериментальных данных n < 50 и состоит из двух частей. Уровень значимости составного критерия является суммой уровней значимости по обеим его частям:

q = q₁ + q₂. (7.3)

Гипотеза по составному критерию принимается, если выполняются условия по двум его частям:

- по первой части проверяется общий разброс экспериментальных данных через среднее значение квантили:

d _1-q1/2 £ d < d _q1/2, (7.4)

где d_1-q1/2 и d_q1/2 - предельно допустимые табличные значения (приложение Ж, таблица 1) при уровнях значимости соответственно 1-q_1/2 и q_1/2:

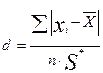(7.5)

- по второй части критерия проверяются концы эмпирического распределения: подсчитываются большие отклонения от среднего:

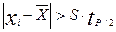(7.6)

где t_p/2 – квантиль функции Лапласа для вероятности P¤2.

Значение вероятности P определяется по приложению Ж, таблице 2 для уровня значимости q_2.

Вторая часть критерия выполняется, если число больших разностей по условию (7.6) не превышает предельно допустимое значение - m (приложение Ж, таблица 2).

Критерий Колмогорова – Смирнова позволяет не только определить соответствие эмпирического распределения теоретическому, но и установить, относятся ли две выборки к одной генеральной совокупности. По критерию оценивается наибольшее расхождение эмпирической и теоретической накопленных относительных частот и функции распределения вероятностей:

D = max çF_{э i} - F_тi ç, (7.7)

где F_эi – накопленная относительная частота в i-том интервале;

F_тi – теоретическая функция распределения вероятностей для i-го интервала.

По значению l:

l = D×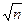 (7.8)

определяется вероятность P(l) по приложению З, с которой можно принять эмпирическое распределение близким к нормальному.

При сопоставлении результатов измерений двух выборок:

D = max çF₁/n₁ – F₂/n₂ ç (7.9)

где F₁, F₂ – накопленные частоты первой и второй выборок;

n₁, n₂ – объёмы выборок:

Гипотеза о принадлежности выборок одной генеральной совокупности принимается, если:

D < D_p, (7.10)

где D_p = 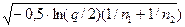(7.11)

При условии, что n₁ +n₂ > 35;

q - уровень значимости.

Критерий Мизеса – Смирнова W² применяют при числе результатов измерений 50 < n < 200. При n > 200 критерий используют, когда проверка по другим критериям не дала однозначного результата. Значение W² рассчитывают по формуле:

W² = -n-2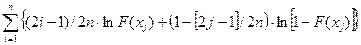 (7.12)

где x_j – результат измерений, имеющий j-й номер в вариационном ряду x₁£x₂£…£x_n;

F(x_j) – значение функции теоретического распределения при значении аргумента x_j (приложение Б, таблица 2).

Вычисляют W² с точностью до 5 значащих цифр, округляя окончательный результат до двух значащих цифр. По таблице приложения И находят значение функции «а», соответствующей вычисленному значению W². Гипотезу о соответствии эмпирического и нормального теоретического распределений принимают, если выполняется неравенство:

a < 1-q (7.13)

где q – заданный уровень значимости. Обычно 0,1 или 0,2.

Приближённые методы проверки оценивают соответствие эмпирического и нормального теоретического распределений сравнением числовых характеристик – асимметрии и эксцесса. Для нормального распределения асимметрия m=0, эксцесс 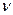=3 (глава 3). Для удобства сравнения используют величину:

E = 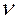-3 = 0 (7.14)

Для эмпирического распределения рассчитывают:

- СКО:

S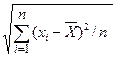^* = ; (7.15)

- третий центральный момент:

m₃ = 1/n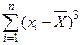; (7.16)

- четвёртый центральный момент:

m₄ = 1/n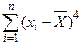; (7.17)

- асимметрию:

m = m₃/(S^*)³ (7.18)

- коэффициент эксцесса:

Е = m₄/(S^*)⁴-3 (7.19)

Рассчитанные значения m и E сравниваются с 0. О малости этих характеристик судят по сравнению с их средними квадратическими погрешностями:

- для асимметрии

m_СКП = 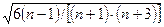(7.20)

- для эксцесса

E_СКП = 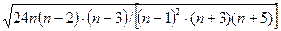(7.21)

Если хотя бы одна из характеристик (m или E) по абсолютному значению в 2-3 раза превосходит свою среднюю квадратическую погрешность, то гипотеза о соответствии эмпирического распределения нормальному теоретическому отклоняется.

Дата добавления: 2014-01-03