Примеры решения задач. ЗадачаВыполните статистическую обработку результатов прямых многократных измерений диаметра отверстия

Задача Выполните статистическую обработку результатов прямых многократных измерений диаметра отверстия, приведенных в таблице 8.1, с доверительной вероятностью Р=0,96, и определите его годность, если размер по чертежу Ø12^+0,035мм. Систематические погрешности исключены.

Таблица 8.1 - Результаты измерений диаметра отверстия

Диаметр отверстия, мм	11,520	11,900	12,010	12,015	12,020	12,028	12,035	12,058	12,985
Число измерений, mi

Решение.

Проверяем ряд результатов измерений на отсутствие промахов.

Среднее арифметическое значение (3.11):

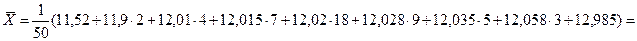
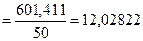(мм)

СКО результатов измерений (3.15):

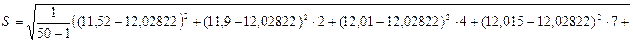
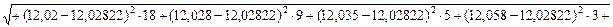
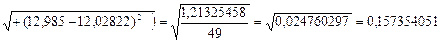(мм)

Проверяем наименьшее и наибольшее значения. Рассчитываем значения квантилей (4.1): ;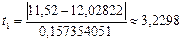

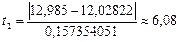
По критерию Шарлье для n=50 предельно допустимое значение к_ш=2,32 (приложение Г). Следовательно, проверяемые значения являются промахами. Их исключаем из вариационного ряда и рассчитываем 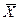и :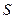

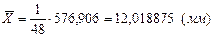
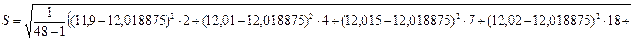
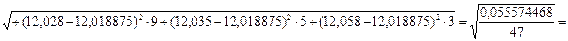
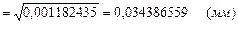
Проверяем значения, оставшиеся крайними в ряду экспериментальных данных: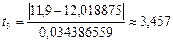

Значение 11,9 исключаем и пересчитываем 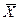и :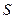

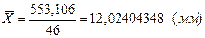
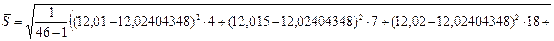
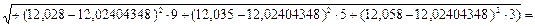
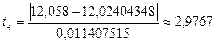
Значение квантиля t₄ также превышает к_ш, поэтому исключаем данные 12,058.

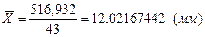
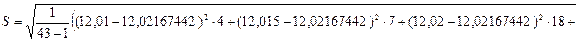
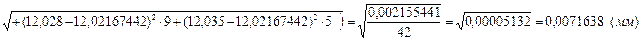Проверяем значение 12.01 мм: 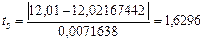, что не превышает значения к_ш=2,32 Следовательно, результат измерений 12,01 мм не является промахом.

Проверяем значение 12,035 мм: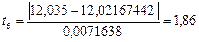

Это значение также не содержит грубых погрешностей и остается в ряду экспериментальных данных.

Проверяем гипотезу о соответствии эмпирического распределения нормальному закону по составному критерию, т.к. n<50.

Критерий 1 – уровень значимости q₁=2%.

По формуле (7.25):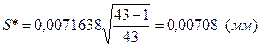

Рассчитываем параметр d (7.5):

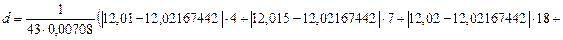
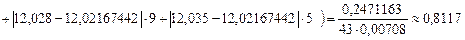
Определяем предельно допустимые значения в по приложению Ж:

; .

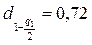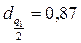Гипотеза по критерию 1 принимается, так как выполняется неравенство (7.4):

Критерий 2 – уровень значимости q₂=2%. По таблице 2 приложения 3 доверительная вероятность Р=0,99.

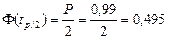
По таблице 1 приложения Б t_p/2=2,575.

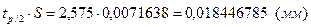
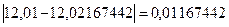(мм); (мм);

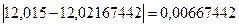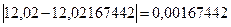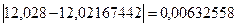(мм); 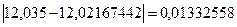(мм);

(мм)

Ни для одного из экспериментальных данных отклонение от среднего не превышает 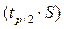, поэтому гипотеза принимается по критерию 2 и в целом по составному критерию.

Рассчитываем доверительный интервал для Р = 0,96 по формуле (3.22).

Коэффициент Стьюдента t_p/2 = 2,055.

;

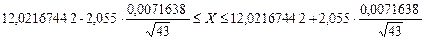
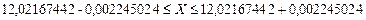
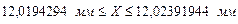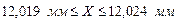
Округление производим до знака, с которым указаны предельно допустимые значения размера.

Предельно допустимые значения диаметра:

D_min = 12,000 мм, D_max = 12,035 мм.

Границы доверительного интервала входят в границы предельно допустимых значений:

12,019 мм > 12,000 мм и 12,024 мм < 12,035 мм, следовательно, диаметр отверстия является годным, так как находится в поле допуска размера.

Задача 8.3.2. Определите электрическую емкость батареи (параллельно соединенных конденсаторов), при доверительной вероятности Р = 0,95, если результаты измерений емкости каждого из них распределены по нормальному закону и представлены в таблице 8.2. Систематические и грубые погрешности исключены.

Таблица 8.2 – Результаты измерений емкости, мкФ

Конденса- № тор измерения	С1	С2	С3	С4
	2,1	5,9	7,6	10,2
	2,8	6,2	7,8	10,5
	2,5	6,4	8,2	10,8
	2,4	6,1	8,6	10,3
	2,2	6,0	7,9	10,0

Решение.

При параллельном соединении емкость батареи конденсаторов имеет линейную зависимость:

С_δ = С₁ + С₂ + С₃ + С₄ (8.16)

Корреляция между погрешностями измерений емкости отсутствует, так как измерения были проведены при включении конденсаторов по отдельности. Применяем алгоритм обработки для линейной зависимости.

Определяем средние арифметические значения и СКО среднего для каждого конденсатора.

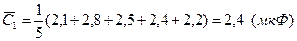
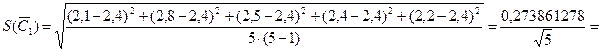
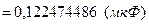
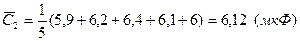
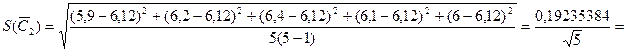
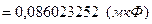
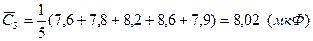
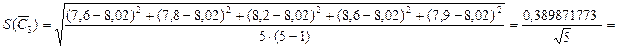
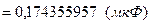
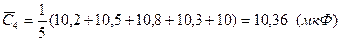
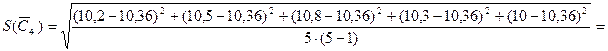
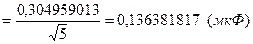
Определяем оценку среднего значения емкости батареи в соответствии с формулой (8.16):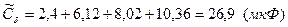

Рассчитываем СКО оценки среднего емкости батареи (8.4):

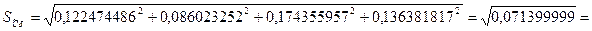
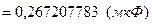
Рассчитываем доверительный интервал (8.12).

Коэффициент Стьюдента для Р = 0,95 и числа степеней свободы, которое при линейной зависимости определяется по формуле:

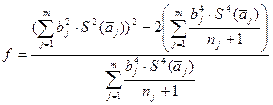(8.17)

где n_j – число измерений a_j - го аргумента, равно:

.

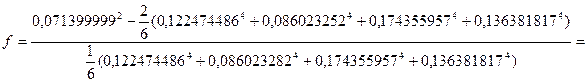
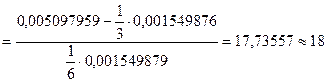По приложению А t_p = 2,11. Доверительный интервал:

;

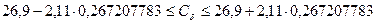
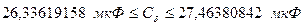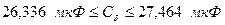
Задача 8.3.3. Определите мощность в электрической цепи по результатам измерений силы тока и напряжения (таблица 8.3), при доверительной вероятности Р = 0,98 и нормальном распределении случайных погрешностей измеряемых аргументов. Систематические и грубые погрешности исключены.

Таблица 8.3 – Результаты измерений параметров электрической цепи

Измеренный пара- № метр измерения	Сила тока, А	Напряжение, В
	5,2	12,6
	5,0	11,8
	5,5	12,0
	5,8	12,7
	4,8	11,9
	5,3	12,5

Решение.

Для определения алгоритма обработки результатов измерений необходимо определить, есть ли корреляция между погрешностями измеряемых аргументов. Рассчитываем средние арифметические значения:

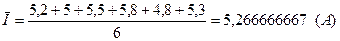
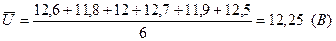
Определяем коэффициент корреляции (8.2):

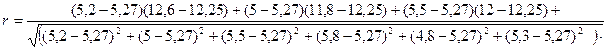
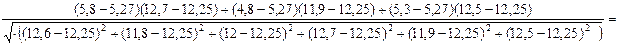
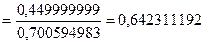
Проверяем условие наличия корреляции (8.1):

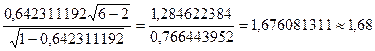
Коэффициент Стьюдента по приложению А для вероятности Р = 0,98 и числа степеней свободы f = n-2 = 6-2 = 4 равен t_p = 3,75, т.е. неравенство (8.1) не выполняется: 1,68 < 3,75, и корреляция отсутствует.

Применяем алгоритм для нелинейной зависимости.

СКО среднего силы тока (8.5):

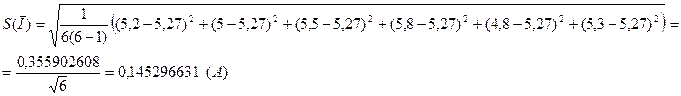СКО среднего напряжения (8.5):

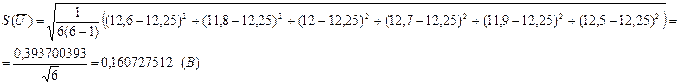Частные производные функциональной зависимости:

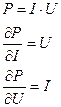(8.18)

(8.19)

(8.20)

СКО среднего мощности (8.6):

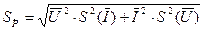(8.21)

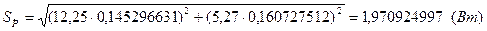
Рассчитываем остаточный член ряда Тейлора и оцениваем его влияние на результат измерений.

Полный дифференциал второго порядка функциональной зависимости (8.18): 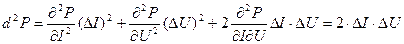(8.22)

где 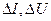- наибольшие(по модулю) отклонения от среднего.

Остаточный член ряда Тейлора (8.7):

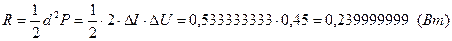
Неравенство (8.8) выполняется:

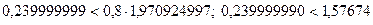
Следовательно, R не влияет на результат измерений и не учитывается.

Оцениваем среднее значение мощности:

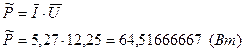(8.23)

Рассчитываем доверительный интервал:

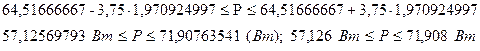
Задача 8.3.4. При поверке гирь посредством измерения их в различных сочетаниях между собой и с эталоном получены показания, приведенные в таблице 8.4. Определите вид измерений и значения каждой из гирь с доверительной вероятностью Р = 0,95.

Таблица 8.4 – Показания весов, г, при сочетании гирь

Сочетания № гирь измерения
x+y	x+y+z	x-y+z	-y+z	-x+z

Решение.

Для каждого сочетания гирь определяем числовые характеристики: среднее арифметическое значение (3.17), дисперсию (3.14), а также статистический вес (8.15).

Для сочетания 1:

-среднее арифметическое значение: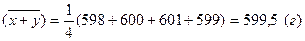

-дисперсия:

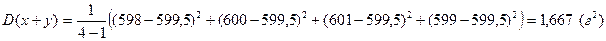
-вес: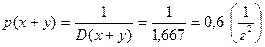

Результаты вычислений по всем сочетаниям представлены в таблице 8.5.

Таблица 8.5 – Числовые характеристики результатов измерений сочетаний гирь.

Сочетания гирь Характеристика
1Среднее арифметическое значение, г	599,5	1600,5	599,75		899,75
2 Дисперсия, г^2	1,667	1,667	2,917	3,333	2,25
3 Вес, 1/г^2	0,6	0,6	0,343	0,3	0,444

Приводим систему из пяти условных уравнений (сочетаний гирь) к системе нормальных уравнений с учетом коэффициентов и весов, представленных в таблице 8.6.

Система нормальных уравнений имеет вид:

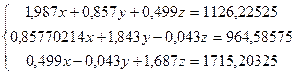(8.24)

Решаем систему через определители. Главный определитель:

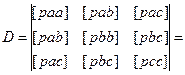(8.25)

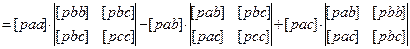
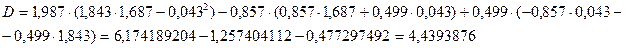Определители для нахождения искомых величин:

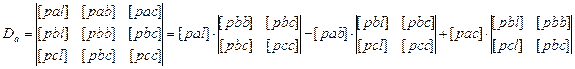(8.26)

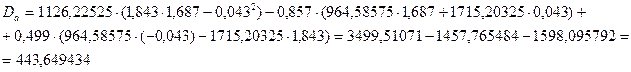
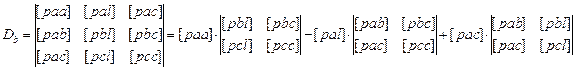(8.27)

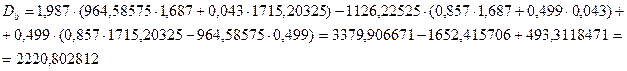
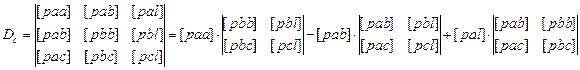(8.28)

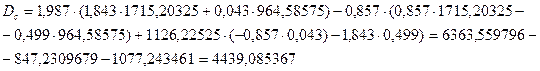
Вычисляем оценки среднего искомых величин:

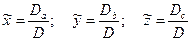(8.29)

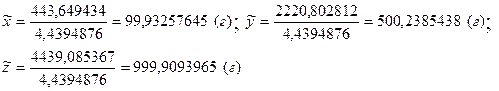
Подставляем значения 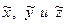в условные уравнения и определяем остаточные погрешности как расхождение левой и правой частей условных уравнений, как показано в таблице 8.7.

Вычисляем СКО остаточных погрешностей по формуле:

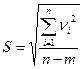(8.30)

где m – число искомых величин (m=3).

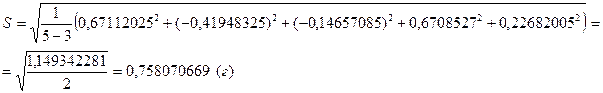
Таблица 8.7 – Определение остаточных погрешностей

Условные уравнения	Остаточные погрешности
Формула определения	Значение

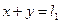
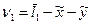
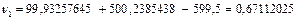
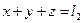
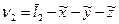
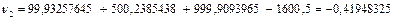
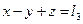
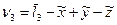
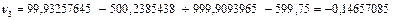
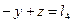
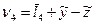
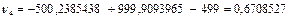
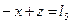
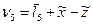
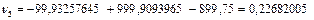
Рассчитываем алгебраические дополнения:

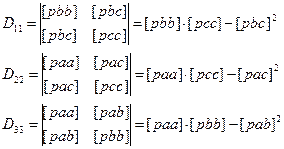(8.31)

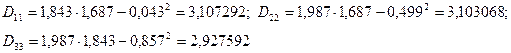
Рассчитываем СКО искомых величин:

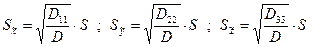(8.32)

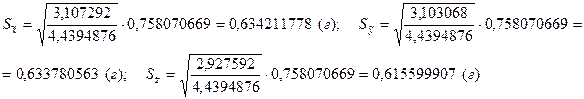
Определяем доверительные интервалы для искомых величин. Коэффициент Стьюдента t_p для доверительной вероятности Р = 0,95 и числа степеней свободы 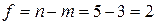равен 4,3:

Дата добавления: 2014-01-03