
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 1.5 Логические основы работы ЭВМ
|
|
|
|
02 1
 0
0
Результат перевода: 134,7510 = 10000110,112
Для перевода чисел из восьмеричной (шестнадцатеричной) системы счисления в двоичную необходимо каждую цифру восьмеричного (шестнадцатеричного) числа представить трехразрядным (четырехразрядным) кодом с помощью таблицы.
Пример:
437, 528= 100 011 111, 101 0102
8FA2, 5Е16 = 1000 1111 1010 0010, 0101 11102
При обратном переводе числа из двоичной системы счисления в восьмеричную или шестнадцатеричную число от запятой влево и вправо разбивается на триады (или по четыре разряда, в случае шестнадцатеричной СС). Если крайние группы получились неполными, их добавляют нулями. Затем каждая полученная группа цифр представляется цифрой той СС, в которую осуществляется перевод.
Пример:
101 011 001, 100 1012 = 531, 458
1010 0111 1000, 1100 00012= А78,С116
Перевод чисел из системы счисления с любым основание в десятичную СС осуществляется по формуле (1).
Для описания функционирования аппаратных и программных средств ЭВМ используется алгебра логики. Алгебра логики оперирует с логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые 1 и 0.
Ранее было отмечено, что основной системой счисления ЭВМ является двоичная СС, к которой используется только две цифры – 0 и 1. Таким образом, одни и те же цифровые устройства ЭВМ могут применяться для обработки как числовой информации в двоичной СС, так и логических переменных.
Совокупность значений логических переменных х1, х2, … хn называется набором переменных.
Функция, равно как и ее аргументы, принимающая значения логической 1 или логического 0 называется логической.
Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 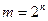 , а число различных функций n аргументов -
, а число различных функций n аргументов - 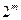
Логические функции одного аргумента представлены в таблице:
| х | Функции | |||
| f1(х) | f2(х) | f3(х) | f4(х) | |
f1(х) = 0 – константа 0, формирование такой функции требует разрыва между входом и выходом;
f2(х) = х, формирование этой функции требует соединения входа с выходом;
 f3(х) = х – функция логического отрицания, инверсия;
f3(х) = х – функция логического отрицания, инверсия;
f4(х) = 1- константа 1, формирование этой функции требует подключения выхода к источнику сигнала логической 1.
Рассмотрим логические функции двух аргументов:
| Аргументы | Функции | ||||||||||||||||
| х1 | х2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Основные логические функции:
1. Логическое отрицание, инверсия, операция НЕ

 f12 = х1, f10 = х2
f12 = х1, f10 = х2
2. Логическое сложение, дизъюнкция, операция ИЛИ
f7 = х1 v х2
3. Логическое умножение, конъюнкция, операция И
f1= х1 ∙ х2
4. Отрицание логического сложения, отрицание дизъюнкции, операции ИЛИ –НЕ
 f8= х1 v х2
f8= х1 v х2
5. Отрицание логического умножения, отрицание конъюнкции, операция И – НЕ
 f14= х1 ∙ х2
f14= х1 ∙ х2
6. Функция неравнозначности, сумма по модулю 2, операция исключающее ИЛИ
 f6= х1 v х2
f6= х1 v х2
Логические функции f0 - f15 являются элементарными логическими функциями.
Основные законы алгебры – логики:
1. Закон двойного отрицания

 х = х
х = х
2. Закон де Моргана


 х1 v х2 = х1 ∙ х2
х1 v х2 = х1 ∙ х2


 х1 ∙ х2 = х1 v х2
х1 ∙ х2 = х1 v х2
Основные тождества алгебры логики:
1. Тождество для инверсии

 0 = 1, 1 = 0
0 = 1, 1 = 0
2. Тождества для дизъюнкции
 1 v х = 1, 0 v х = х, х v х = х, х v х =1
1 v х = 1, 0 v х = х, х v х = х, х v х =1
3. Тождества для конъюнкции
 1 ∙ х = х, 0 ∙ х = 0, х ∙ х = х, х ∙ х = 0
1 ∙ х = х, 0 ∙ х = 0, х ∙ х = х, х ∙ х = 0
Логическое устройство, реализующее работу какой- либо функции, называется логическим элементом.
Общее условно – графическое обозначение (УГО) логических элементов:

* - функция, которую выполняет логический элемент
УГО и таблицы истинности основных логических элементов:
элемент НЕ элемент ИЛИ элемент И элемент ИЛИ-НЕ элемент И-НЕ
|
|





|




 | |||||||||||||||||
 | |||||||||||||||||
 |  | ||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
НЕ
| х |  х х
|
ИЛИ ИЛИ-НЕ
| х1 | х2 | х1 v х2 |
И
| х1 | х2 | х1 ∙ х2 |
| х1 | х2 |  х1 v х2 х1 v х2
|
И-НЕ
| х1 | х2 |  х1 ∙ х2 х1 ∙ х2
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 416; Нарушение авторских прав?; Мы поможем в написании вашей работы!