Понятие корреляции рангов

Указанные выше показатели оценки степени тесноты корреляционной связи между признаками относятся к параметрическим. Основой непараметрических методов является принцип нумерации вариант (индивидуальных значений) статистического ряда.
Значения признака располагаются по возрастанию (или убыванию). Каждой единице такого ряда присваивается порядковый номер в ряду. Причем номер первый получает наименьшая (или, наоборот, наибольшая) варианта, номер второй получает следующая по величине варианта и т.д. Эти порядковые номера индивидуальных значений (вариант) изучаемого признака, расположенные в ряду в порядке возрастания или убывания своей величины, называются рангами. Затем ранги (порядковые номера) индивидуальных значений факторного признака располагают в порядке возрастания (убывания) и с ними сопоставляются соответствующие ранги (порядковые номера) индивидуальных значений результативного признака. Для повторяющихся индивидуальных значений признака ранг определяется как средняя арифметическая соответствующих номеров. Например, если одинаковые по величине значения признака занимают в ранжированном ряде третье и четвертое места, то ранг (порядковый номер) для каждого из них будет равен.

Наличие связи между признаками в данном случае можно получить, если сопоставить последовательность взаимного расположения рангов факторного и результативного признаков. Если с возрастанием величины рангов факторного признака х соответствующие им величины рангов результативного признака у обнаруживают тенденцию к увеличению, можно сделать вывод о наличии прямой (положительной) связи. Если же с увеличением рангов факторного признака ранги результативного признака уменьшаются, то это свидетельствует о возможном наличии между изучаемыми признаками обратной связи. Из многочисленных непараметрических методов оценки степени тесноты связи наибольшее применение в статистическом анализе корреляционной зависимости нашли коэффициенты корреляции рангов, разработанные К. Спирменом и М. Кэнделлом.

Коэффициент корреляции рангов Спирмена (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле (12.22):

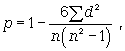(12.22)

где d = N_x - N_y, т.е. разность рангов каждой пары значений х и у; n - число наблюдений.

Ранговый коэффициент корреляции Кэнделла (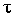) можно определить по формуле (12.23):

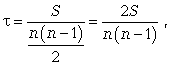(12.23)

где S = P + Q.

Существует также множественный коэффициент ранговой корреляции (коэффициент конкордации), который используется для определения тесноты связи между произвольным числом ранжированных признаков (12.24):

W = 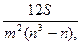(12.24)

где m – количество факторов; n – число наблюдений; S – отклонение суммы квадратов рангов от средней квадратов рангов.

Дата добавления: 2014-01-03