Статистические методы выявления корреляционной связи

Тема 12. Корреляционный метод анализа

Зависимость между факторными и результативными признаками может быть функциональной или корреляционной. Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативного признака, т.е. каждому значению признака-фактора соответствует строго определенное значение результативного признака. В корреляционной связи между изменением факторного и результативного признака такого полного соответствия нет, воздействие факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Выделяют также стохастические связи, т. е. зависимости, проявляющиеся не в каждом отдельном случае, а в среднем, при большом числе наблюдений. Корреляционные связи считаются частным случаем стохастической связи.

При исследовании корреляционных зависимостей решается широкий круг вопросов:

1) предварительный анализ свойств изучаемой совокупности;

2) установление факта наличия связи, определение ее направления и формы;

3) измерение степени тесноты связи между признаками;

4) нахождение аналитического (математического) выражения связи или построение регрессионной модели;

5) оценка адекватности модели, ее интерпретации и практическое использование.

При проведении корреляционно-регрессионного анализа должны соблюдаться определенные требования:

1) качественную однородность изучаемой совокупности следует дополнить количественными характеристиками совокупности с применением показателей вариации и проверкой гипотезы о принадлежности выделяющихся или аномальных значений признака исследуемой совокупности;

2) исходные данные должны быть массивными, представительными;

3) включаемые в исследование признаки-факторы должны быть основными (оказывать решающее влияние на уровень результативного признака) и быть независимыми друг от друга (не должны дублировать друг друга);

4) при практическом применении результатов изучения корреляционной связи следует иметь в виду, что все основные положения теории корреляции и регрессии разрабатывались исходя из предложения о нормальном характере распределения рассматриваемых признаков.

Характеристика основных методов изучения взаимосвязей представлена в таблице 12.1.

Таблица 12.1 – Методы изучения взаимосвязей

Методы	Характеристика
1. Индексный метод	Позволяет определить роль отдельных факторов в совокупном измерении сложного явления. С помощью взаимосвязанных индексов выясняют, как изменились результативные показатели в связи с изменением показателей-факторов
2. Метод параллельных рядов	Полученные в результате сводки и обработки материалы располагаются виде параллельных рядов и сопоставляются между собой для установления характера и тесноты связи
3. Балансовый метод	Данные взаимосвязанных показателей изображаются в виде таблицы и располагаются таким образом, что бы итоги между отдельными её частями были равны
4. Метод аналитических группировок	Единицы статистической совокупности группируются, и для каждой группы рассчитывается средняя или относительная величина по результативному признаку; затем изменение средних или относительных значений результативного признака сопоставляются с изменениями факторного признака для выявления характера связи между ними
5. Дисперсионный анализ	Даёт возможность определить значение систематической и случайной вариации, а также установить роль конкретного фактора в изменении результативного признака
6. Корреляционное отношение	Сопоставление межгрупповой дисперсии с общей называется корреляционным; оно характеризует долю вариации результативного признака, вызванную действием факторного признака, положенного в основание группировки
7. Корреляционно-регрессионный анализ	Позволяет оценить тесноту и направление связи между результативными и факторными показателями и получить уравнение зависимости результативного показателя от показателей-факторов. Задачи корреляционного анализа – измерить тесноту связи между варьирующими признаками, определить неизвестные причинные связи и оценить факторы, оказывающие наибольшее влияние на результативный признак. Задачи регрессионного анализа – установить формы зависимости, определить функции регрессии и использовать уравнения для оценки неизвестных значений зависимой переменной

12.2 Статистические исследования формы корреляционной связи. Основные этапы корреляционного анализа

Форма корреляционной связи в основном определяется с помощью теоретического анализа, однако в ряде случаев приходится только предполагать наличие определённой формы связи. Эти предположения в последствии проверяют при помощи графического анализа.

В корреляционно-регрессионном анализе используются различные формы связи (12.1, 12.2, 12.3, 12.4):

1) прямолинейная

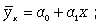(12.1)

2) криволинейная в виде:

- параболы второго порядка (или высших порядков)

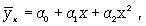(12.2)

- гиперболы

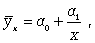(12.3)

- показательной функции

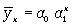(12.4) и т.д.

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у. Важнейшей задачей при этом является определение формы связи с последующим расчетом параметров уравнения, или, иначе, нахождение уравнения связи.

Уравнение парной линейной регрессии (12.5):

Уi теор = ао + а1 * хi. (12.5)

Параметры связи в этом уравнении, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК) (12.6):

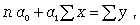
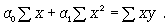(12.6)

Если связь выражена параболой второго порядка (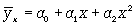), то систему нормальных уравнений для отыскания параметров a₀, a₁, a₂ можно представить в виде (12.7):

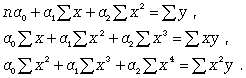(12.7)

Такую связь называют множественной линейной регрессией.

Выделяют также нелинейную регрессию, которая бывает двух классов:

1) регрессии нелинейные относительно включённых в исследование переменных, но линейные по параметрам;

2) нелинейность по оцениваемым параметрам.

Для оценки нелинейной регрессии чаще всего используют коэффициент эластичности (12.8), который показывает, на сколько процентов изменится у при изменении х на один процент:

Э = dУ/dХ * Х/У или Э = а1*х / у (для линейного уравнения). (12.8)

Выделяют следующие этапы анализа линейной корреляционной зависимости:

1) сбор и подготовка исходных данных;

2) построение поля корреляции;

3) выбор формы связи;

4) оценка тесноты связи.

5) оценка коэффициента корреляции на достоверность.

Указанная оценка может быть проведена по коэффициенту значимости Стьюдента (12.9):

t расч = 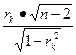. (12.9)

При этом должно выполняться условие:

tрасч > tтаб (tтаб берётся из таблицы коэффициентов Стьюдента).

6) расчет коэффициентов регрессии для уравнения ух = ах + b(12.10, 12.11):

a = ;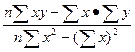

b = 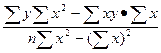. (12.10, 12.11)

7) расчет доверительных пределов отклонений.

Доверительные пределы отклонений (+/- d) – это расстояния вверх и вниз от теоретической линии, образующие доверительную область виде полосы вдоль теоретической линии, в которую с заданной вероятностью будут попадать все уi (12.12):

+/- d = +/- t таб 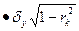. (12.12)

8) оценка предсказательной силы модели – осуществляется по двум критериям:

- остаточной дисперсии (оценка ведётся по коэффициенту вариации) (12.13):

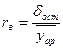(12.13);

Для экономических прогнозов коэффициент вариации должен быть меньше или равен 10%.

- критерию Фишера (12.14):

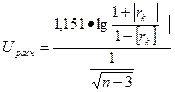. (12.14)

Если 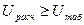, то предсказательная сила модели достаточная.

При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней нескольких рядов динамики. Применение для этого методов классической теории корреляции связано с определенными особенностями:

1) в рядах динамики зачастую наблюдается зависимость между последующими и предшествующими уровнями. Наличие такой связи в статистической литературе называют автокорреляцией. При изучении взаимосвязи между рядами динамики с применением методов корреляционно-регрессионного анализа автокорреляция должна быть исключена из каждого из сравниваемых рядов динамики;

2) в изменении уровней нескольких рядов динамики, как правило, существует лаг, т.е. смещение во времени по сравнению с изменением уровней другого ряда динамики. Для получения более правильной оценки степени тесноты корреляционной связи также необходимо исключить этот лаг, т.е. нужно сдвинуть уровни одного ряда относительно другого на некоторый промежуток времени;

3) условия формирования уровней рассматриваемых рядов, как правило, изменяются. Соответственно может изменяться во времени и степень тесноты связи. В этих условиях речь идет о переменной корреляции.

Таким образом, при анализе корреляционной связи между рядами динамики необходимо:

1) измерить связь между предыдущими и последующими уровнями;

2) с учетом указанных выше особенностей изучить связь между рядами динамики.

Первая задача решается по каждому ряду динамики: в качестве факторного признака рассматриваются фактические уровни ряда, а уровни этого же ряда со сдвигом на один период принимаются в качестве результативного признака. Исчисляются коэффициенты автокорреляции и авторегрессии, при этом коэффициент автокорреляции рассчитывается на основе формулы коэффициента линейной (парной) корреляции. Если результаты расчета коэффициентов автокорреляции будут указывать на наличие автокорреляции уровней исходных рядов динамики, то для дальнейшего анализа корреляционной связи между рядами динамики нужно эту автокорреляцию исключить.

12.3 Статистическое измерение тесноты корреляционной связи

При изучении корреляционной связи важным направлением анализа является также оценка степени тесноты связи, для чего используется две группы методов:

1) параметрические – основаны на использовании оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения (корреляционные методы);

2) непереметрические – не накладывают ограничения на закон распределения изучаемых величин.

Показатели тесноты связи должны удовлетворять ряду основных требований:

• величина показателя степени тесноты связи должна быть равна или близка к нулю, если связь между изучаемыми признаками (процессами, явлениями) отсутствует;
• при наличии между изучаемыми признаками (х и у) функциональной связи величина степень тесноты связи равна единице;
• при наличии между признаками (х и у) корреляционной связи показатель тесноты связи выражается правильной дробью, которая по величине тем больше, чем теснее связь между изучаемыми признаками (стремится к единице);

· при прямолинейной корреляционной связи показатели тесноты связи отражают и направление связи: знак (+) означаетналичие прямой (положительной) связи; а знак (-) – обратной (отрицательной).

Измерение тесноты зависимости для всех форм связи может быть осуществлено при помощи вычисления эмпирического корреляционного отношения 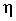(12.15):

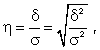(12.9)

где - 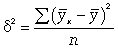дисперсия в ряду выравненных значений результативного показателя ;

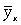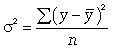- дисперсия в ряду фактических значений у.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать две следующие формулы (12.16, 12.17):

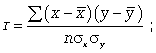(12.16, 12.17)

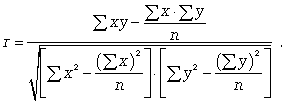
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости. Выводы о тесноте связи можно сделать по шкале Чаддока:

1) при r от 0,1 до 0,3 связь слабая;

2) при r от 0,3 до 0,5 связь умеренная;

3) при r от 0,5 до 0,7 связь заметная;

4) при r от 0,7 до 0,9 связь высокая;

5) при r от 0,9 до 0,99 связь весьма высокая.

Все указанные выше коэффициенты служат для оценок связей количественных признаков. Для оценок связи качественных признаков используются следующие коэффициенты:

1) коэффициент ассоциации используется для определения тесноты связи двух качественных признаков, состоящих из двух групп; его можно рассчитать по формуле (12.18):

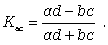(12.18)

2) коэффициент контингенции также используется для определения тесноты связи двух качественных признаков, состоящих из двух групп, и рассчитывается по формуле (12.19):

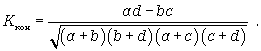(12.19)

Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации. Связь считается подтверждённой, если Касс > 0,5 или Ккон>0,3.

3) если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (К_П).

Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы (таблица 12.2).

Таблица 12.2 – Вспомогательная таблица для расчета коэффициента взаимной сопряжённости

Признаки	A	B	C	Итого
D	m11	m12	m13	∑m1j
E	m21	m22	m23	∑m2j
F	m31	m32	m33	∑m3j
Итого	∑mj1	∑mj2	∑mj3	П

Здесь m_ij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.

Коэффициент взаимной сопряженности Пирсона определяется по формуле (12.20):

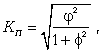(12.20)

где 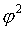- показатель средней квадратической сопряженности:

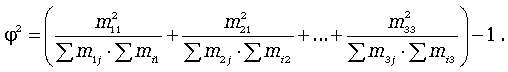
Коэффициент взаимной сопряженности изменяется от 0 до 1; в статистике существуют различные его модификации.

4) коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле(12.21):

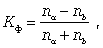(12.21)

где n_a - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; n_b - соответственно количество несовпадений.

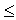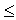Коэффициент Фехнера может изменяться в пределах -1,0 К_ф +1,0.

Дата добавления: 2014-01-03