Воспроизводимость процессов и МШС

Прежде всего надо определиться с самим понятием «шесть сигма». Для этого необходимо ввести понятие воспроизводимости процесса – Ср.

Индекс воспроизводимости — безразмерная величина, показывающая связь между характеристиками технологического процесса и допуском.

Пусть USL и LSL — соответственно верхняя и нижняя границы поля допуска, а 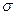— среднеквадратичное отклонение показателя качества в технологическом процессе. Тогда, если показатель имеет нормальное распределение и его среднее значение находится в середине поля допуска, индекс воспроизводимости С_р определяется по формуле

С_p = (USL–LSL)/ 6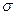 (6.1),

где при контроле технологического процесса с помощью контрольных карт в качестве несмещенной оценки стандартного отклонения принимается величина

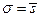/c (6.2),

если расчет ведется через стандартные отклонения, или

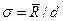(6.3),

если используются размахи.

В этих условиях при С_p = 1 вероятность брака теоретически составляет 0,27% (см. рис. 6.2); при этом доля несоответствующих изделий составит при этом 27/10000 = 2700 изделий на миллион, т.е. 2700 ppm (ppm — parts per million — единица измерения уровня несоответствий).

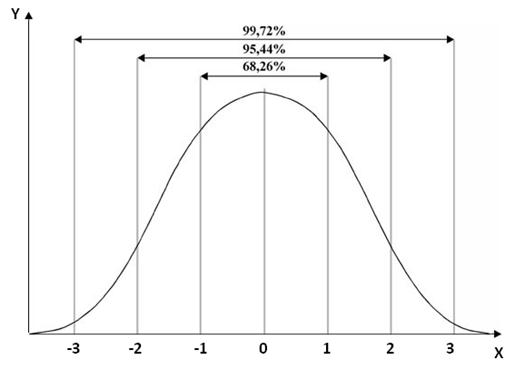
Рис.6.2 – Симметричное распределение при ± три сигма

Стандарт рекомендует в качестве минимально приемлемого значения С_p = 1,33 (дефектность составит 63 ppm). При С_р = 1,67 уровень несоответствий составит 6 ppm, а при С_p = 2, когда поле допуска вдвое шире диапазона рассеивания технологического процесса, — 2 изделия на миллиард.

Часто используется обратная величина, иногда называемая коэффициентом точности,

k_T=l/C_p. (6.4)

Он вычисляется в процентах и показывает часть поля допуска, покрываемую рассеиванием процесса. Например, С = 1,33 соответствует 75% поля допуска.

При одностороннем допуске вместо формулы (6.1) используют соответственно верхний индекс воспроизводимости.

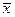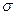C_pu= (USL – )/ 3 (6.5)

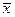( — средний уровень настройки процесса), или нижний индекс воспроизводимости

C_pl = (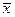–LSL)/ 3 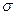(6.6)

Индекс воспроизводимости (6.1) предполагает точное центрирование процесса — совпадение среднего значения 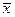с целевым уровнем 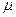. Для учета расхождения между характери­стиками вводится индекс центрированности к:

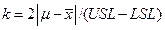(6.7)

при точном центрировании к = 0, при совпадении среднего уровня с одной из границ поля допуска к = 1.

Индекс работоспособности процесса (иногда называется индексом настроенности или налаженности)

Cpk=Cp(1–k) (6.8)

не превышает индекса воспроизводимости.

На рисунке 6.3 показаны четыре возможные ситуации с точки зрения работоспособности процесса: а)процесс воспроизводим и центрирован;

б) процесс воспроизводим, но не центрирован, требует настройки; в) процесс невоспроизводим, г) процесс невоспроизводим и не центрирован. В последних двух случаях для обеспечения работоспособности процесса, как правило, усилий рабочего не достаточно, требуется вмешательство менеджеров высокого уровня.

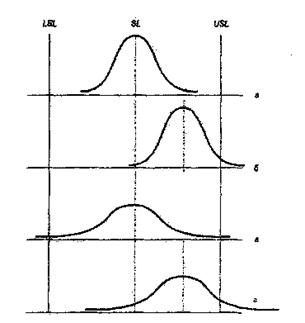
Рис. 6.3 – Анализ работоспособности процесса

Рассмотренные показатели применимы для оценки возможностей процесса в том случае, если с использованием контрольных карт подтверждена статистическая управляемость процесса. Для индивидуальных наблюдений дополнительно необходимо убедиться в нормальности распределения контролируемого показателя. В таблице 6.1 приводится связь числа дефектных изделий со значением С_p. При размахе 12 сигм число дефектных равно 2 дефектам на миллиард при строгой симметрии распределения.

Таблица 6.1 – Зависимость числа дефектных при возрастании разброса

№ п/п	Сp	Сигма	% нахождения в зоне	Число дефектных на 10^6
		±3	99,73
	1,33	±4	99,9964
	1,67	±5	99,999957	0,57
	2,0	±6	99,99999998	0,0002
	Со сдвигом	6±1,5	99,99966	3,4

Однако, специалисты Моторола посчитали, что среднее значение может отличаться от целевого на 1,5 сигма, тогда число дефектных на миллион равняется 3,4. Эта цифра принята за норму и все расчеты, связывающие качество процессов с выходом годных ведутся из расчета 3,4 dpm (дефектов на миллион). Эта ситуация иллюстрируется на рисунке 6.4.

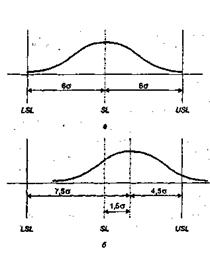
Рис.6.4 – Расчет несоответствий в МШС

Для получения наилучшей воспроизводимости процесса необходимо выполнение двух условий:

1. Действительное среднее процесса должно располагаться как можно ближе к целевому значению или к среднему ГС.

2. Разброс значений процесса должен быть меньше функциональных границ.

Цель любого проекта МШС удовлетворять всем основным требованиям с высокой степенью точности. Существует две возможности: улучшение процесса ШС и использование ДФСС (см. параграф 6.4).

Дата добавления: 2014-01-03