Закон сохранения энергии

Закон сохранения энергии, является основным законом движения воздуха по горным выработкам. При выводе основного закона принимают, что его объемный вес остается постоянным, т. е. рассматривают воздух как несжимаемый. Это ведет к погрешности, которая не более 7-10 %.

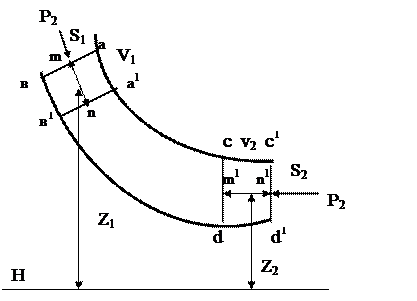
Рис.5.5 Схема к выводу уравнения Бернулли для струйки воздуха в выработке

В элементарной струйке тока выделим объем, а b с d (рис.5.5). Элементарная струйка тока это струйка настолько малого поперечного сечения, что скорость движения воздуха в любом ее сечении постоянна. Элементарная струйка тока ограничена линиями тока. Линия тока это геометрическое место точек, касательная в любой точке есть вектор скорости потока. Через некоторое время dt объем переместится и займет положение a¹b¹c¹d¹. Площадь поперечного сечения струйки в ab S₁, в cd S_2, давление соответственно Р₁, Р₂. В предположении не сжимаемости потока воздуха перемещение объема воздуха a b c d в положение a¹b¹c¹d¹ можно рассматривать как перемещение объема воздуха abb¹a¹ в положение cd d¹c¹ при неизменном положении объема a¹b¹cd. Принимая во внимание закон сохранения энергии, запишем, что приращение кинетической энергии указанного объема равно работе внешних сил, т.е.

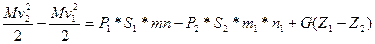, (5.24)

где М и G – соответственно масса и вес элементарного объема воздуха. В равенстве (5.24) S₁*mn=V₁, а S₂*m¹n¹=V₂ и V₁=V₂=V-объем воздуха.

V=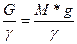 (5.25)

С учетом равенства (5.25) будем иметь

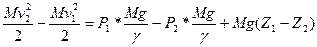, (5.26)

Сгруппировав члены с однородными индексами, получим уравнение Бернулли для идеальных жидкостей и газов

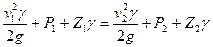(5.27)

В действительности при движении воздуха по выработкам имеет место трение его о стенки выработок. Обозначим потерю давления на трение через h. Кроме этого необходимо учесть, что в процессе движения воздуха по выработкам изменяется его объемный вес, т. е. γ ≠ const. Тогда равенство (5.27) запишется в виде

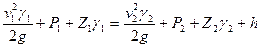(5.28)

Из равенства (5.28) следует, что разность давлений, расходуемая на преодоление сопротивления сети горных выработок, определяется по формуле

h=(P₁-P₂)+(Z₁ γ₁-Z₂ γ₂)+(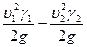) (5.29)

Равенство (5.29) является общим выражением закона движения воздуха по горным выработкам.

В этом равенстве (P₁-P₂)-разность давлений, создаваемая вентилятором;

(Z₁ γ₁-Z₂γ₂)-разность весов столбов воздуха, которая называется естественной тягой;

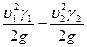()-скоростной напор;

Тогда получим

h=h_в±h_е±h_ск (5.30)

Из равенства (5.30)следует, что разность давлений, расходуемая вентилятором на преодоление сопротивления сети горных выработок движущимся по ним воздухом, слагается из перепада давления, создаваемого вентилятором, естественной тягой и скоростным напором. Причем в общем случае естественная тяга может способствовать или противодействовать работе вентилятора, входное и выходное сечение потока могут отличаться по величине, что учитывается знаком перед h_{е и} h_ск

Дата добавления: 2014-01-03