Пример расчета. Систему уравнений (6.57) (6.58) можно решить графически

Графический метод

Систему уравнений (6.57) (6.58) можно решить графически. Для этого, задаваясь произвольным значением «Y» (например 1,2,3 и т. д.) и подставляя его в равенство (6.57) находим значение «Х». По полученным данным строим гиперболу, описываемую уравнением (6.57).

Аналогично задаваясь произвольным значением «х» и подставляя их в уравнение (6.58) получаем значение «y» и строим гиперболу, описываемую уравнением (6.58). Координаты точки пересечения этих графиков и дадут решение системы.

Заданы сопротивления ветвей простого диагонального соединения и общая депрессия соединения. Определить, расходы воздуха во всех ветвях соединения и сделать проверку полученного результата, используя второй закон расчета вентиляционных сетей

Дано: R₁=0.8 km; R₂=0.12 km; R₃=0.2 km; R₄=0.36 km; R₅=0.45 km H=300 кг/м²

Определить; Q,q₁, q_2, q₃, q_4, q_5.

Решение задачи

Определим направление движения воздуха в диагонали 2-3.

В нашем примере R₁/R₃=0.8/0.2=4.0, а R₂/R₄=0.12/0.36=0.33, следовательно

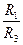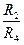>и воздух в диагонали будет двигаться от узла 3 к узлу 2. В этом случае, согласно, необходимо изменить обозначения сопротивлений ветвей диагонального соединения, так как показано на рис.6.14

Вычислим по равенствам (6.56) значения вспомогательных величин a,b,c,d.

a=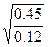=1.936 b=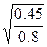=0.75 c=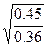=1.12 d=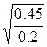=1.5

С учетом полученных значений вспомогательных величин равенства (6.57) (6.58) можно записать в виде

x=0.75 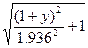(6.74) y=1.12 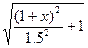(6.75)

Систему уравнений (6.74) (6.75) решаем методом последовательных приближений. Задаемся первоначальным значением x=x₀=1.5 и из уравнения (6.75) определяем значение y₁=2.17. По уравнению (6.74) определяем значение x₁=1.44 и т. д. y₂=2.14, x₂=1.43, y₃=2.13. Дальнейшие вычисления не имеют смысла. Окончательно принимаем x=1.43, y=2.13

Так как, по условию задачи задана общая депрессия соединения, то для опреде­ления общего расхода воздуха и потоков воздуха в ветвях необходимо определить, общее сопротивление диагонального соединения по формуле (6.72)

R₀=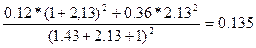km

Определим общий расход воздуха в сети по формуле (6.73)

Q₀=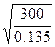=47.1 м³/с

Определяем поток воздуха в диагонали по формуле (6.60), а потоки воздуха в остальных ветвях по формулам (6.61-6.64)

q₅=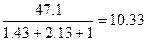м³/с

q₂=q_5*x=10.33*1.43=14.77 м³/с; q₃=q₅*y=10.33*2.13=22.0 м³/с

q₁=q₃+q₅=22.0+10.33=32.33 м³/с q₄=q₂+q₅=14.77+10.33= 25.1 м³/с

Проверяем правильность полученного распределения воздуха, используя второй закон расчета вентиляционных сетей.

Для контура 1-2-3-1 должно выполнятся равенство (6.53), а для контура 2-4-3-2 равенство (6.54)

0.8*14.77^2- 0.45*10.33²-0.12*32.33²=0,07=0

0.2*25.1² - 0.36*22.0² +0.45*10.33²=-0,2=0

Незначительная невязка по депрессии связана с округлениями при вычислениях.

Дата добавления: 2014-01-03