Методика расчета распределения воздуха в сложной вентиляционной сети

Задана вентиляционная сеть произвольной сложности, а также общее количество воздуха или тип вентилятора для проветривания шахты. Необходимо определить расходы воздуха во всех ветвях соединения.

Для любого элементарного контура вентиляционной сети всегда выполняются 1-й и 2-й законы расчета вентиляционных сетей:

∑q_i=0 (7.1)

∑h_i=0 (7.2)

∑h_i+∑p_i=0 (7.3)

где ∑q_i-сумма расходов воздуха в узле;

∑h_i- алгебраическая сумма депрессий ветвей элементарного контура;

∑p_i- алгебраическая сумма давлений, создаваемая вентиляторами во всех ветвях замкнутого контура.

Задача о распределении воздуха в сложной вентиляционной сети решается методом последовательных приближений. Он заключается в том, что первоначальное распределение воздуха задается произвольно, однако в целом по контуру или для узла сети оно должно подчиняться уравнению неразрывности потока, т.е. равенству (7.1).

Первоначально произвольно принятое значение расхода воздуха в ветви q_i отличается от действительного q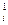на некоторую величину ∆q_i. Тогда депрессия любой ветви h_i может быть выражена равенством:

h_i=R_i q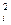= R_i (q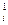+∆q_i)² (7.4)

Раскрывая скобки правой части равенства, получим

h_i= R_i (q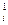)²+2 R_i q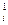∆q_i+ R_i (∆q_i)² (7.5)

Полагая, что ∆q_i мало, отбрасываем тем более малую величину R_i (∆q_i)² и из равенства (7.5) определяем величину ошибки для одной ветви

∆q_i=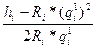 (7.6)

Для всех ветвей, входящих в элементарный контур величина ошибки определится по формуле

∆q_i=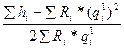 (7.7)

С учетом равенства (7.3), согласно которому ∑h_i=-∑p_i, окончательно получим

∆q_i=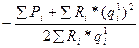 (7.8)

где 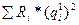-алгебраическая сумма депрессий ветвей замкнутого контура;

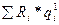-сумма произведений R_i на q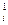по всем ветвям, взятая без учета направления потока;

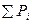-алгебраическая сумма давлений, создаваемая вентиляторами во всех ветвях замкнутого контура.

При расчете распределения воздуха в сложной вентиляционной сети необходимо выполнять следующие правила:

1. Обход каждого элементарного контура выполнять по часовой стрелке;

2. Потоки, направленные по часовой стрелке считаются положительными, против часовой стрелки отрицательными;

3. Если величина ошибки (поправки) рассчитанная по формуле (7.8) положительна (>0), то она суммируется с потоками воздуха, направление которых совпадает с направлением обхода контура и вычитается из расходов направленных против направления обхода контура;

4. Если величина ошибки имеет отрицательный знак, она вычитается из потоков воздуха, направление которых совпадает с направлением обхода контура и суммируется с противоположными потоками;

5. Если величина ошибки по абсолютному значению больше первоначально принятого расхода воздуха и вычитается из него, это значит, что первоначально принятое направление воздуха неверно и его необходимо изменить на противоположное направление.

6. Расчет выполняется несколько раз, пока последующие расходы воздуха будут отличаться от предыдущих расходов с требуемой степенью точности.

Дата добавления: 2014-01-03