Правила решения для одномерных производственных функций

Предположим, есть один ресурс (который может быть аппаратными средствами, программным обеспечением, трудом или капиталом, и так далее), который допускает производство информации или изделий, относящихся к сфере коммуникаций (которые могут быть фактическими информационными записями, или сделками, или сообщениями, или даже программными средствами). Производственная функция описывает функциональное отношение между количеством ресурса R и количеством продукта I, и записывается как

I=I(R)

Отношение между I и R может быть линейным (постоянный коэффициент), или иметь возрастающее или убывающее отношение. Это зависит от того, как увеличение в ресурсе производит сравнительно меньше или больше продукции.

Случай 1: Проверка закона Гроша

Рассмотрим закон Гроша, где R – капитал для покупки некоторой компьютерной мощности, и продукт I - компьютерная мощность. Закон Гроша может быть записан следующим образом:

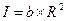
где b – это снова некоторая константа прямой пропорциональности. Какой это тип производственной функции?

Ответ

Эта производственная функция имеет возрастающий масштаб. Увеличение в два раза ресурса R (расход капитала возрастает дважды) имеет в качестве результата увеличение в четыре раза I (что означает умножение компьютерной мощности на фактор 4).

Другие примеры производственных функций:

I = Количество строк кода (Человеко-Месяцы), в разработке программного обеспечения и

I = Количество сделок (Количество процессоров), в работе системы управления распределенной базы данных.

Поведение производственных функций может быть изучено посредством следующих инструментов. Прежде всего, средняя производительность, получаемая делением продукта на ресурс:

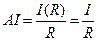
Предельная производительность – это сумма изменений в продукте dI, вызванных небольшим бесконечно малым изменением в ресурсе dR, заканчивающемся классической производной функцией:

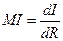
Рассматривая как простое приложение производственную функцию с постоянным коэффициентом, говорят:

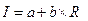
В этом случае, MI = b, в то время как AI дано:

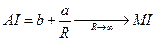
которое иногда ведет к интерпретации, что предельная производительность является средней производительностью “длительного периода”.

Интересен следующим общий результат

Свойство

Средняя производительность является оптимальной, когда предельная производительность равняется средней производительности.

Доказательство: дана оптимальная средняя производительность:

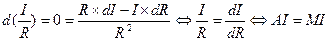
Следующий график может быть типичным поведением производственной функции

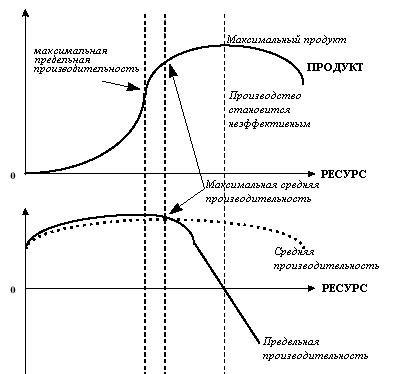
Рис. 2. Свойства одномерной производственной функции

Очевидный вопрос – как максимизировать доходы в случае конкретной одномерной производственной функции. Конечно, для того, чтобы ответить на этот вопрос, должны быть известны доходы на единицу продукции, и предполагает, что дано:

q=q(t)

в случае, когда доходы на единицу продукции зависят от времени. Аналогично, стоимость единицы ресурса может быть обозначена:

p=p(t)

и в случае, если и доход и затраты независимы от времени, они просто задаются:

q(t)=q^o (константа) и p(t)=p^o (константа)

Функция прибыли в пределах конкретного инвестиционного горизонта дана при дисконтированном денежном потоке издержек и доходов перед продуктов и ресурсов. В конкретном случае это задается так:

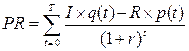
Проблема управленческого решения для такой производственной функции должна решаться в оптимальном производстве, которое означает такое, которое приносит максимальную прибыль.

Предложение

Прибыль максимальна, когда предельная производительность равна

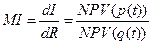
Доказательство: прибыль максимальна, когда

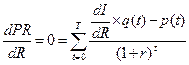
или, при преобразовании, когда

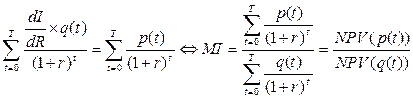
Следствие

В случае, когда p и q независимы от времени, оптимальное производство задается так

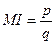
Случай 2: Обучение в сравнении с производством

Предположим, что организация имеет бюджет человеко-мощности, который равняется N человеко-месяцам. Работники в организации производят с начальной производительностью p единиц за человеко-месяц. Кривая обучения может быть определена как функция p(n), которая показывает, как производительность растет в результате обучения в течение n человеко-месяцев. Конечно, p(0) = p. По определению p(n) – монотонно возрастающая функция (в противном случае "обучение" не имеет смысла?). Найдите оптимальные усилия на обучение.

Ответ

Общее производство, очевидно, является функцией от человеко-месяцев n, потраченных на обучение. Так производственная функция для этого случая задается как

P(n) = (N - n) x p(n)

Ясно, что должен существовать некий оптимум, с тех пор как задано начальное производство

P(0) = N x p(0) = N x p

и, конечно, расход всего доступного времени на обучение является не очень продуктивным:

P(N) = 0 x p(N) = 0!

Например, когда p(n) = 4 + 3 x n и N = 30, рисунок 3 показывает функцию P(n).

Оптимальное количество обучения n* задается так

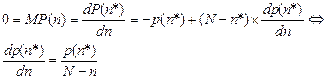
что должно быть решено для n*. В случае линейной функции обучения, это может быть сделано очень просто. На самом деле, если p(n)=a+bxn, тогда

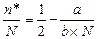
Альтернативой для производственной функции является функция издержек, в которой ресурс смоделирован как функция от количества продуктов, которые должны быть поставлены. В этом случае, количество ресурсов выражается как функция количества продуктов, которые должны быть произведены, говорят, что

R=R(I)

Предельная стоимость определена как

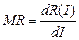
В этом случае, аналогичные правила решений могут быть сформулированы, чтобы определить оптимальное количество продуктов, которые могут быть затребованы для данной функции затрат, следующим образом.

Прибыль максимальна, когда предельные издержки равны

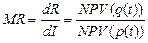
Дата добавления: 2014-01-03