Понятие определенного интеграла

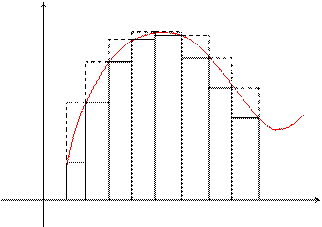
Пусть на отрезке [ a, b ] задана непрерывная функция f(x).

y

M

m

0 a x_i b x

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [ a, b ]

Разобьем отрезок [ a, b ] на части (не обязательно одинаковые) n точками.

x ₀ < x ₁ < x ₂ < … < x_n

Тогда x ₁ – x ₀ = D x ₁, x ₂ – x ₁ = D x ₂, …, x_n – x_{n -1} = D x_n;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

[ x ₀, x ₁] ® m ₁, M ₁; [ x ₁, x ₂] ® m ₂, M ₂; … [ x_{n -1}, x_n ] ® m_n, M_n.

Составим суммы:

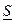_n = m ₁D x ₁ + m ₂D x ₂ + … + m_n D x_n =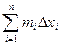

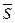_n = M ₁D x ₁ + M ₂D x ₂ + … + M_n D x_n =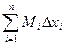

Сумма 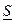называется нижней интегральной суммой, а сумма 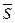– верхней интегральной суммой.

Т.к. m_i £ M_i, то 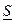_n £ 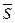_n, а m(b – a) £ 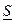_n £ 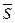_n £ M(b – a)

Внутри каждого отрезка выберем некоторую точку e.

x ₀ < e₁ < x ₁, x ₁ < e < x ₂, …, x_{n -1} < e < x_n.

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [ a, b ].

S_n = f(e₁)Dx₁ + f(e₂)Dx₂ + … + f(e_n)Dx_n =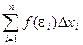

Тогда можно записать: m_iDx_i £ f(e_i)Dx_i £ M_iDx_i

Следовательно, ,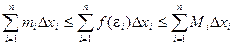

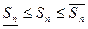
Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.

Обозначим maxDx_i – наибольший отрезок разбиения, а minDx_i – наименьший. Если maxDx_i® 0, то число отрезков разбиения отрезка [ a, b ] стремится к бесконечности.

Если 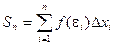, то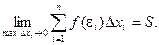

Если при любых разбиениях отрезка [ a, b ] таких, что maxDx_i® 0 и произвольном выборе точек e_i интегральная сумма 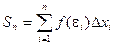стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [ a, b ].

Обозначается: 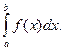, где

а – нижний предел интегрирования, b – верхний предел интегрирования, х – переменная интегрирования, [ a, b ] – отрезок интегрирования.

Пусть функция F(x) является первообразной для функции f(x) на некотором промежутке D, а числа a и b принадлежат этому промежутку.

Приращение F(b) – F(a) любых из первообразных функций F(x) + С при изменении аргумента от х=а до х=b называется определенным интегралом от функции f.

Вычисляется определенный интеграл по формуле Ньютона – Лейбница:

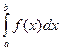= F(b) – F(a)

Дата добавления: 2014-01-03