
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства общего решения
|
|
|
|
1) Т.к. постоянная С – произвольная величина, то, вообще говоря, дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Частным решением дифференциального уравнения называется решение, полученное из общего решения при фиксированных значениях постоянной.
Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши(теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную 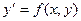 , то какова бы не была точка (х0, у0) в области D, существует единственное решение
, то какова бы не была точка (х0, у0) в области D, существует единственное решение 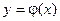 уравнения
уравнения 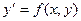 , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
, определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
Пример. Найти общее решение дифференциального уравнения 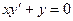 .
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
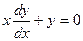
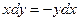
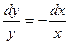
Теперь интегрируем: 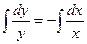
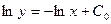
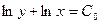
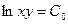
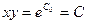
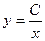 - общее решение исходного дифференциального уравнения.
- общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
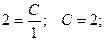
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
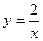
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка у ′ = f (x, y) называется уравнением с разделяющимися переменными, если его можно представить в виде:
у ′ = f 1(x) ∙ f 2(y).
При решении дифференциальных уравнений с разделяющимися переменными полезно придерживаться следующей схемы:
- разделить переменные (т.е. в одной части уравнения должно быть выражение, содержащее только переменную х, в другой – переменную у);
- найти интегралы от обеих частей уравнения, найти частное решение уравнения;
- найти частное решение, удовлетворяющее начальным условиям (если они заданы).
Пример. Найти общее решение дифференциального уравнения: ydy + xdx = 0
Сначала разделим переменные, т.е. запишем уравнение в виде
ydy = -xdx,
затем найдем интегралы от обеих частей уравнения:
∫ ydy = -∫xdx,
получим 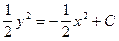
Пример. Найти общее решение дифференциального уравнения: 2 уу ′ = 1-3 х 2.
Заменим у ′ = 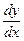 и умножим обе части уравнения на dx.
и умножим обе части уравнения на dx.
Получим: 2 уdy = (1-3 х 2) dx,
Затем найдем интегралы от обеих частей:
2∫ уdy = ∫(1-3 х 2) dx,
у 2 = х - х 3+ С.
Пример. Найти частное решение дифференциального уравнения (решить задачу Коши для заданных начальных условий): (1+ x 2) dy – 2 x (y +3) dx = 0, если у = -1 при х = 0.
Сначала найдем общее решение. Разделим переменные (для этого выражение (– 2 x (y +3) dx) перенесем в правую часть и разделим обе части уравнения на (1+ x 2)(y +3)).
Получим: 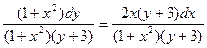 ,
,
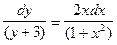 ,
,
найдем интегралы от обеих частей:
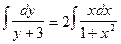
Вычислим отдельно каждый интеграл.
1.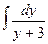 . Введем новую переменную t = у +3, тогда dt = (у +3) ′∙ dу = dу, т.е. dt = dу. Подставим новую переменную в интеграл:
. Введем новую переменную t = у +3, тогда dt = (у +3) ′∙ dу = dу, т.е. dt = dу. Подставим новую переменную в интеграл:
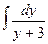 =
= 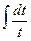 = ln
= ln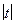 +C = ln
+C = ln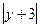 + C
+ C
2. 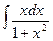 . Введем новую переменную t = 1+ x 2 , тогда dt = (1+ x 2) ′∙ dx = 2 xdx, откуда d x =
. Введем новую переменную t = 1+ x 2 , тогда dt = (1+ x 2) ′∙ dx = 2 xdx, откуда d x = 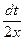 . Подставим новую переменную в интеграл:
. Подставим новую переменную в интеграл:
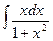 =
= 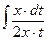 =
= 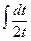 =
= 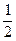 ln
ln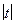 +C =
+C = 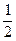 ln
ln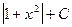
Найдем общее решение данного уравнения:
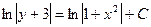
Для нахождения частного решения подставим в общее решение вместо х и у заданные начальные значения: 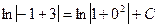 ,
,
найдем С: С = ln 2,
подставим в общее решение получившееся значение C:
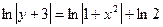
Пример. Найти общее решение дифференциального уравнения: 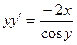
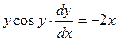
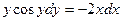
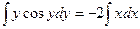
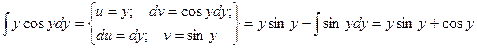

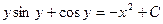
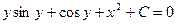 -
-
это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Пример. Найти решение дифференциального уравнения 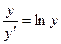 при условии у (2)= 1.
при условии у (2)= 1.
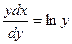
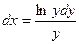
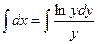
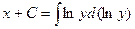
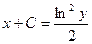
при у (2) = 1 получаем 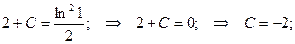
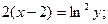 или
или 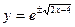 - частное решение;
- частное решение;
Пример. Решить уравнение 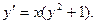
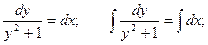
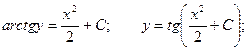
Пример. Решить уравнение 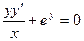 при условии у(1) = 0.
при условии у(1) = 0.
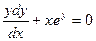
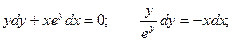
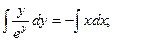
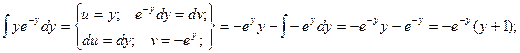
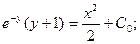
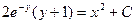
Если у(1) = 0, то 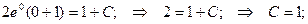
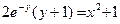 .
.
Пример. Решить уравнение 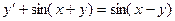 .
.
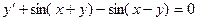
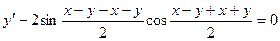
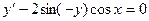
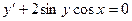
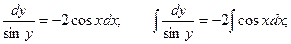
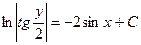
Пример. Решить уравнение 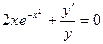
Преобразуем заданное уравнение:
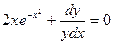
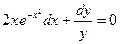
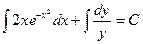
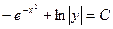
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 931; Нарушение авторских прав?; Мы поможем в написании вашей работы!