Представление полинома Жегалкина в каноническом виде.Представление булевой функции над базисом называется каноническим полиномом (многочленом) Жегалкина

Операция двоичного сложения. Многочлены Жегалкина

Алгебра 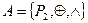называется алгеброй Жегалкина. Российский математик Жегалкин И.И. (1869-1947) предложил логическую связь, отраженную в таблице 15, называть суммой х и у и обозначать .

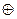Таблица 15

х	у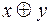

В алгебре высказываний сумма истинна тогда и только тогда, когда истинно только одно составляющее сложного высказывания.

Можно также провести аналогию между операцией сложения по mod 2 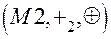и операцией двоичного сложения. Действительно, 0+0=0

0+1=1

1+0=1

1+1=(1)0, т.е. операция двоичного сложения в пределах последнего двоичного порядка имеет ту же последовательность символов, что и сумма по модулю два. Поэтому операция М2 имеет особое значение в схемах контроля и исправления ошибок. Если один из аргументов из-за неисправности в схеме исказится, то и значение функции изменится на противоположное.

Число полиномов Жегалкина от n переменных составляет 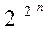, т.е. равно числу булевых функций от тех же переменных.

Теорема (Жегалкин И.И.) Всякая булева функция единственным образом представима в виде полинома Жегалкина.

Единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях.

Представление полинома Жегалкина в каноническом виде выглядит следующим образом:

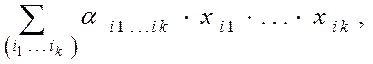
где 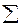- сложение по модулю два; знак (∙) обозначает конъюнкцию;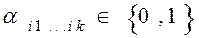

Канонический полином Жегалкина от двух переменных имеет вид:

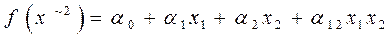
от трех переменных:

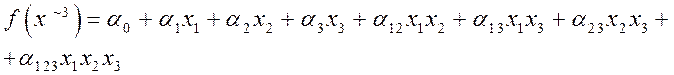Любой полином Жегалкина может быть приведен к каноническому виду.

Пример14. Привести многочлен Жегалкина к каноническому виду.

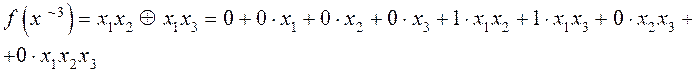т.е.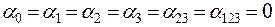

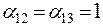
Дата добавления: 2014-01-03