К полиному Жегалкина

Некоторые методы перехода от булевых функций

Указанная выше единственность представления булевой функции полиномом Жегалкина позволяет применять разнообразные методы построения соответствующих данной функции полиномиальных выражений, заботясь лишь о том, чтобы результирующий полином был приведенным, т.е. не содержал одинаковых сомножителей в конъюнкциях и одинаковых слагаемых. Ниже приводятся некоторые из них:

1. Метод, базирующийся на эквивалентном преобразовании формул заключается в следующем:

- представить функцию 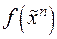формулой над множеством связок 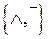и произвести эквивалентные преобразования, использую соотношения:

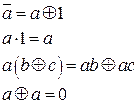
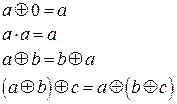
Здесь a, b, c обозначают как переменную, так и формулы.

Пример 15. Привести к полиному Жегалкина функцию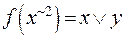

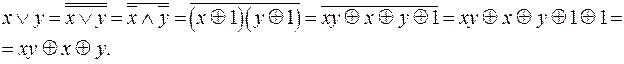
2. Достаточно часто используется метод неопределенных коэффициентов. Рассмотрим его на примере.

Пример 16. Пусть 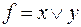. Использую формулу полинома Жегалкина для двух переменных и придавая х, у возможные значения, выпишем систему уравнений для коэффициентов:

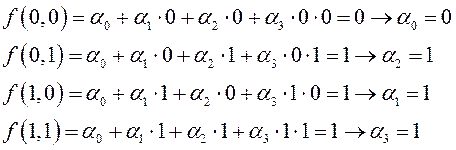
Следовательно, 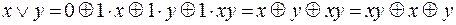, т.е. мы получим тот же полином Жегалкина, что и в примере 15.

3. Переход от функции, представленной в виде СДНФ, к полиному Жегалкина.

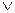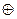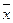При переходе от булевой функции, представленной в СДНФ, можно заменить знак на знак , а на 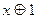, а затем привести полученное выражение к такому виду, чтобы в нем не было одинаковых сомножителей в конъюнкциях и одинаковых слагаемых.

Пример 17. Перейти от СДНФ булевой функции 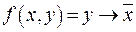к полиному Жегалкина в каноническом виде.

1. Построим для 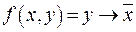таблицу истинности.

Таблица 16

х	у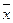

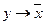
2. Найдем СДНФ: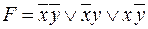

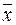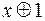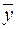3. Заменив на , на 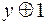и знак 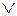на знак 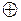получим:

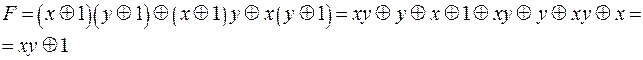
Проверим правильность построения полинома Жегалкина по таблице истинности

Таблица 17

х	у	ху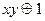

Т.к. итоговые столбцы таблиц 16 и 17 совпадают, то преобразование произведено верно.

Приведем полученный полином Жегалкина к каноническому виду:

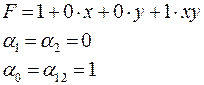
Имеются и другие методы перехода от булевой функции к полиному Жегалкина.

Используя любой из методов перехода можно представить каждую булеву функцию полиномом Жегалкина.

Ниже приведено представление булевых функций от двух переменных полиномами Жегалкина.

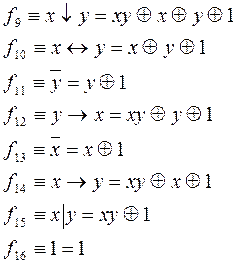
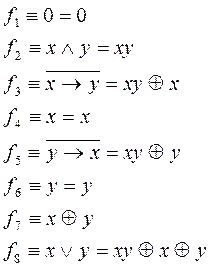
В справедливости вышеприведенных соотношений следует убедиться самостоятельно, используя различные методы перехода от булевой функции к полиному Жегалкина, а затем произвести проверку путем построения таблицы истинности для левой и правой части формул.

РАЗДЕЛ 2. МНОЖЕСТВА И ОТОБРАЖЕНИЯ

Дата добавления: 2014-01-03