Основные понятия теории множеств. Понятие множества является одним из наиболее общих математических понятий

Тема 2.1 Множества

Понятие множества является одним из наиболее общих математических понятий. Его определение не удается свести к другим понятиям. Поэтому для понятия множества дается описательное определение, содержание и смысл которого раскрываются при изучении теории множеств.

Множество – это набор, совокупность каких-либо объектов, называемых его элементами, обладающих некоторым общим для них характеристическим свойством. В качестве примеров можно привести множество действительных чисел, множество решений заданного алгебраического уравнения, множество прямых, проходящих через заданную точку. В принципе никаких ограничений на природу элементов, их количество и свойства не налагается, так что допустимо рассмотрение таких множеств, как множество налогоплательщиков, множество процентных ставок и т. п.

Элементы, составляющие множество, обычно обозначаются малыми латинскими буквами, а само множество – большой латинской буквой. Знак 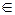используется для обозначения принадлежности элемента множеству. Запись a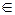A означает, что элемент a принадлежит множеству A. Если некоторый объект x не является элементом множества A, пишут x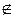A. Например, если A – это множество четных чисел, то 2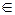A, а 1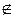A. Множества A и B считаются равными (пишут A=B), если они состоят из одних и тех же элементов.

Элементы, из которых состоит данное множество, сами могут быть множествами. Например, рассмотрим множество студенческих групп на втором курсе. Его элементами являются группы. Каждая группа – это множество студентов.

Если множество содержит конечное число элементов, его называют конечным; в противном случае множество называется бесконечным. Если множество A конечно, символом |A| будет обозначаться число его элементов. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом 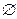. Очевидно, |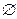|=0.

Множества А и В называются эквивалентными, если существует взаимно-однозначное соответствие между множествами А и В. Эквивалентные, или равномощные, множества обозначаются .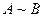

Если 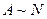, то множество А называется счетным. Счетное множество – это такое множество А, все элементы которого могут быть занумерованы в бесконечную последовательность 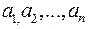так, чтобы при этом каждый элемент получил лишь один номер n и каждое натуральное число n было бы номером лишь одного элемента множества А. Таким образом, счетное множество – это множество значений какой-либо последовательности . Пустое множество по определению относится к счетным.

Конечное множество может быть задано перечислением всех его элементов. Если множество A состоит из элементов x, y, z, …, пишут A={x, y, z, …}.

Пример 1. A = {0, 2, 4, 6, 8} – множество четных десятичных цифр;

B = {2, 3} – множество решений уравнения x²–5x+6=0;

C = {0, 1, 2, 3, 4, 5, 6} – множество остатков при делении целых чисел на 7.

Иногда перечислением элементов задают и бесконечное множество. Это делают в тех случаях, когда ясен алгоритм последовательного порождения элементов:

A={0, 1, 4, 9, 16, …} – множество квадратов целых чисел.

В общем случае множества можно определять по так называемой схеме свертывания. При заданном характеристическом свойстве F и заданном классе элементов K множество A определяется как множество, которое содержит все элементы из K, обладающие свойством F. Для определения по схеме свертывания используется следующая запись:

A = {x | x обладает свойством F}.

Применяя сокращение F(x) для обозначения того, что элемент x обладает свойством F, будем писать

A = {x | F(x)}.

Класс K может быть указан явно; в этом случае используется запись

A = {x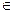K | F(x)}.

Множество четных чисел P можно определить как

P = {x | x – четное целое число},

или как

P = { x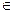Z | x четно},

где через Z обозначено множество целых чисел.

Неограниченное применение схемы свертывания ведет к противоречиям. Например, можно получить «множество всех множеств»:

M = {x | x – множество}.

Если считать M множеством, то получаем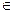 MM.

Рассмотрим парадокс Рассела, открытый в 1902 году. Назовем множество правильным, если оно не является своим элементом, и неправильным в противном случае. Определим множество R как множество всех правильных множеств. Более формально:

R = {x | x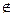R}.

В соответствии с определением для любого множества A справедливо утверждение:

A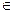R тогда и только тогда, когда A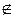A. В частности, если считать R множеством, то его само можно взять в качестве A, но тогда мы придем к противоречию:

R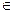R тогда и только тогда, когда 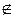RR.

Более подробно. Если R правильное, то есть не является своим элементом, то оно должно находиться в R, то есть быть своим элементом. Если же R неправильное, то оно является своим элементом, то есть содержится в R, но R содержит только правильные множества. Таким образом, R не может быть ни правильным, ни неправильным.

Введем используемое в дальнейшем понятие индексированного семейства множеств. Пусть I – некоторое множество, каждому элементу которого i сопоставлено однозначно определенное множество A_i. Элементы множества I называют индексами, а совокупность множеств A_iназывают индексированным семейством множеств и обозначают через (A_i)_i∈I.

Подмножества. Говорят, что множество B является подмножеством (или частью) множества A и пишут BA, если всякий элемент множества B является элементом множества A. Например, множество натуральных чисел N является подмножеством множества целых чисел Z, а последнее, в свою очередь, является подмножеством множества рациональных чисел Q, то есть NZ и ZQ, или, короче, NZQ. Легко видеть, что если BA и AB, то множества A и B состоят из одних и тех же элементов, и, значит, A=B. Наряду с обозначением BA используется также A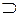B, имеющее тот же смысл.

Вообще говоря, подмножество множества A может быть задано определяющим свойством. Например, свойство быть четным числом определяет в множестве целых чисел подмножество четных чисел. Каково бы ни было множество A, пустое множество и само A являются его подмножествами: 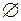A, AA. Пустое множество может быть задано свойством, которым не обладает ни один элемент множества A, например, x≠x. Возможны и более содержательные ситуации. Например, свойство быть корнем уравнения x²+1=0 задает в множестве действительных чисел пустое подмножество. Множество A может быть задано как свое подмножество каким-нибудь свойством, которым обладают все элементы множества A, например, x = x. Подмножества множества A, отличные от 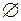и A, называются собственными. Совокупность всех подмножеств множества А называется булеаном,или множеством-степенью, и обозначается Р(А) или 2^А.

Пример 2. Пусть A={a, b, c}. Тогда множество 2^А состоит из следующих элементов:

{∅}, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.

Если множество A конечно и содержит n элементов, то это множество имеет 2ⁿ подмножеств, то есть |2^А |= 2 ^|A|.

Множество всех подмножеств, находящихся в рассмотрении, называется универсальным, или универсумом, и обозначается через U.

Дата добавления: 2014-01-03