
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над множествами. Пересечение множеств A и B, обозначаемое AB, – это множество, состоящее из всех тех элементов, которые принадлежат обоим множествам A и B
|
|
|
|
Пересечение множеств A и B, обозначаемое A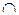 B, – это множество, состоящее из всех тех элементов, которые принадлежат обоим множествам A и B.
B, – это множество, состоящее из всех тех элементов, которые принадлежат обоим множествам A и B.
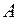
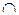
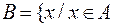 и
и 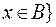 .
.
Например, если A={1,2,3} и B={2,3,4}, то A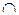 B={2,3}. В соответствии с определением, A
B={2,3}. В соответствии с определением, A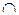 B
B A и A
A и A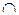 B
B B, причем, A
B, причем, A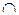 B является в определенном смысле наибольшим множеством, обладающим этими свойствами: если C
B является в определенном смысле наибольшим множеством, обладающим этими свойствами: если C A и C
A и C B, то C
B, то C A
A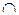 B. Если С={x: x имеет рост выше 180 см} и D={x: x любит играть в шахматы}, тогда
B. Если С={x: x имеет рост выше 180 см} и D={x: x любит играть в шахматы}, тогда 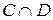 ={x: x имеет рост выше 180 см и любит играть в шахматы}.
={x: x имеет рост выше 180 см и любит играть в шахматы}.
Далее, A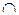 B=B тогда и только тогда, когда B
B=B тогда и только тогда, когда B A. Если множества A и B не имеют общих элементов, их пересечение пусто, A
A. Если множества A и B не имеют общих элементов, их пересечение пусто, A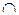 B=∅; в этом случае говорят, что множества A и B не пересекаются.
B=∅; в этом случае говорят, что множества A и B не пересекаются.
Пересечение множеств А и В называется также их произведением и обозначается 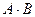 .
.
Объединение множеств A и B, обозначаемое как A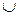 B, – это множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств A и B. Это определение равносильно следующему:
B, – это множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств A и B. Это определение равносильно следующему: 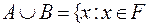 или
или 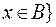 . Например, если A={1,2,3} и B={2,3,4}, то A
. Например, если A={1,2,3} и B={2,3,4}, то A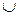 B={1,2,3,4}. В соответствии с определением A
B={1,2,3,4}. В соответствии с определением A A
A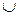 B и B
B и B A
A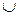 B, причем A
B, причем A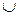 B является наименьшим множеством, обладающим этими свойствами: если A
B является наименьшим множеством, обладающим этими свойствами: если A C и B
C и B C, то A
C, то A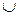 B
B C.
C.
Операции пересечения и объединения можно обобщить на случай произвольного индексированного семейства множеств.
Разностью множеств 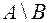 называется множество всех тех, и только тех элементов А, которые не содержатся в В. Или что то же самое:
называется множество всех тех, и только тех элементов А, которые не содержатся в В. Или что то же самое:
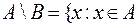 и
и 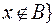 .
.
Например, 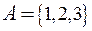 ,
, 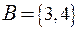 ,
,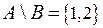 .
.
Симметрическая разность множеств А и В, обозначаемая 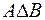 , есть множество
, есть множество 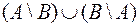 .
.
Например, если А={1,2,4,6,7}, В={2,3,4,5,6}, то А\В={1,7}, а 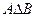 ={1,3,5,7}.
={1,3,5,7}.
Симметрическая разность состоит из тех элементов, которые принадлежат в точности одному из двух множеств А или В. Если А={x: x играет в теннис}, а В={x: x играет в гольф}, то А\В={x: x играет в теннис, но не играет в гольф}, 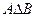 ={x: x играет только в теннис или играет только в гольф}.
={x: x играет только в теннис или играет только в гольф}.
Симметрическая разность называется иначе кольцевой суммой 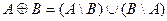 . Из определения симметрической разности вытекает равенство, связывающее её с ранее введенными операциями:
. Из определения симметрической разности вытекает равенство, связывающее её с ранее введенными операциями: 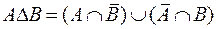 .
.
Например, если A={1,2,3} и B={2,3,4}, то A\B={1}. В соответствии с определением A\B A и (A\B)
A и (A\B) 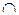 B=
B=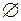 , причем A\B является в определенном смысле наибольшим множеством, обладающим этими свойствами: если C
, причем A\B является в определенном смысле наибольшим множеством, обладающим этими свойствами: если C A и C
A и C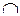 B=
B=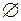 , то C⊂A\B.
, то C⊂A\B.
Дополнение множества А, обозначаемое 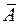 , - это множество элементов универсума, которые не принадлежат А. Следовательно,
, - это множество элементов универсума, которые не принадлежат А. Следовательно, 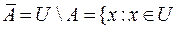 и
и 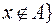 .
.
Если U- множество положительных чисел, а A={2,4,6,8,…}- множество всех положительных четных чисел, то 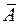 ={1,3,5,7,…}- множество всех положительных нечетных чисел. Если А={x: x – любитель научной фантастики}, тогда
={1,3,5,7,…}- множество всех положительных нечетных чисел. Если А={x: x – любитель научной фантастики}, тогда 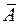 ={x: x – не любит научную фантастику}.
={x: x – не любит научную фантастику}.
Декартовым (прямым) произведением множеств А и В называется множество 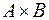 , состоящее из всех упорядоченных пар элементов, в которых первый элемент принадлежит А, а второй принадлежит В, т.е.
, состоящее из всех упорядоченных пар элементов, в которых первый элемент принадлежит А, а второй принадлежит В, т.е. 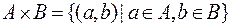 .
.
Упорядоченная пара – это одно из исходных, неопределяемых понятий. Интуитивно это понятие определяется как совокупность, состоящая из двух элементов a и b, расположенных в определенном порядке. Две упорядоченные пары (a,b) и (c,d) называются равными, если a=c и b=d.
Если множество состоит из n элементов: А={a1, a2, …, an}, то элементы a1, a2, …, an называются компонентами или координатами n-ки. Упорядоченная n-ка называется также кортежем из элементов a1, a2, …, an.
Координаты точек на плоскости – это упорядоченная пара чисел, координаты точки в пространстве – упорядоченная тройка чисел, кортеж автомобилей при сопровождении официального лица или очередь их желающих посетить выставку - это также примеры упорядоченных наборов элементов.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 2872; Нарушение авторских прав?; Мы поможем в написании вашей работы!