Бинарные отношения

Тема 2.2 Отображения

В повседневной жизни нам постоянно приходится сталкиваться с понятием «отношения». Отношения – один из способов задания взаимосвязей между элементами множества.

Унарные (одноместные) отношения отражают наличие какого-то одного признака R у элементов множества M (например, «быть красным» на множестве шаров в урне).

Бинарные (двуместные) отношения используются для определения взаимо

связей, которыми характеризуются пары элементов во множестве M.

Например, на множестве людей могут быть заданы следующие отношения: «жить в одном городе», «x работает под руководством y», «быть сыном», «быть старше» и т.д. на множестве чисел: «число a больше числа b», «число a является делителем числа b», «числа a и b дают одинаковый остаток при делении на 3».

В прямом произведении 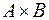, где A - множество студентов какого-либо вуза, B - множество изучаемых предметов, можно выделить большое подмножество упорядоченных пар (a, b), обладающих свойством: «студент a изучает предмет b». Построенное подмножество отражает отношение «изучает», возникающее между множествами студентов и предметов. Число примеров можно продолжить

Отношения между двумя объектами являются предметом исследования экономики, географии, биологии, физики, лингвистики, математики и других наук.

Для строгого математического описания любых связей между элементами двух множеств вводится понятие бинарного отношения.

Бинарным отношением между множествами A и B называется подмножество R прямого произведения 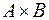. В том случае, когда 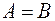можно просто говорить об отношении R на A.

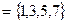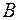
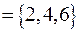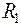
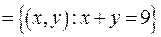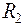
Пример 1. Выпишите упорядоченные пары, принадлежащие бинарным отношениям R₁ и R₂, заданными на множествах A и : , 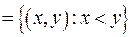. Подмножество R₁ состоит из пар: 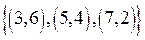. Подмножество .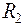

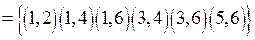Область определения R на 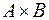есть множество всех элементов из A таких, что для некоторых элементов 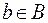имеем 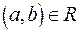. Иными словами область определения R есть множество всех первых координат упорядоченных пар из R.

Множество значений отношения R на 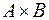есть множество всех 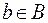таких, что 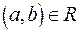для некоторых 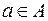. Другими словами множество значений R есть множество всех вторых координат упорядоченных пар из R.

В примере 1 для R₁ область определения: 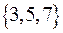, множество значений - 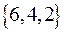. Для R₂ область определения: 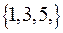, множество значений: .

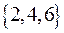Во многих случаях удобно использовать графическое изображение бинарного отношения. Оно осуществляется двумя способами: с помощью точек на плоскости и с помощью стрелок.

В первом случае выбирают две взаимно перпендикулярные линии в качестве горизонтальной и вертикальной осей. На горизонтальной оси откладывают элементы множества A и через каждую точку проводят вертикальную линию. На вертикальной оси откладывают элементы множества B, через каждую точку проводят горизонтальную линию. Точки пересечения горизонтальных и вертикальных линий изображают элементы прямого произведения .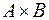

Пример 5. Пусть , .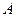

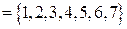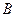
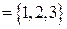Пусть R₁ задано на 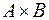перечислением упорядоченных пар: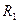 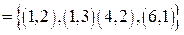. Бинарное отношение R₂ на множестве 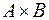задано с помощью правила: упорядочена пара 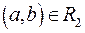, если a делится на b. Тогда R₂ состоит из пар: .

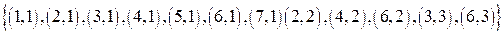Бинарные отношения, из примера 2, R₁ и R₂ изображены графически на рис. 6 и рис.7.

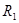
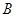
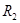
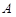
Рис. 6 Рис. 7

Чтобы изобразить бинарное отношение с помощью стрелок, слева изображаются точками элементы множества A, справа - множества B. Для каждой пары (a, b), содержащейся в бинарном отношении R, проводится стрелка от a к b,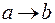. Графическое изображение бинарного отношения R₁, приведенного в примере 6, показано на рис.8.

Рис.8

Бинарные отношения на конечных множествах могут быть заданы матрицами. Предположим, что задано бинарное отношение R между множествами A и B. , .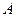

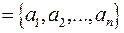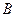
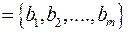Строки матрицы нумеруются элементами множества A, а столбцы – элементами множества B. Ячейку матрицы, стоящую на пересечении i - ой строки и j - ого столбца принято обозначать через C_ij, а заполняется она следующим образом:

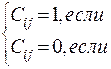
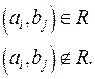
Полученная матрица будет иметь размер .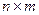

Пример 6. Пусть задано множество 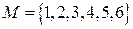. На множестве задайте списком и матрицей отношение R – «быть строго меньше».

Отношение R как множество содержит все пары элементов (a, b) из M такие, что .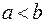

.

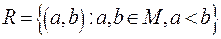Тогда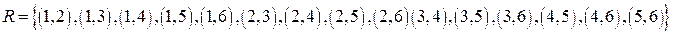

Матрица отношения, построенная по вышеуказанным правилам, имеет следующий вид:

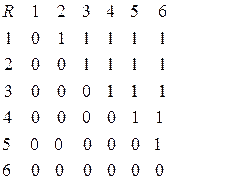
Свойства бинарных отношений:

1. Бинарное отношение R на множестве 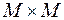называется рефлексивным, если для любого элемента a из M пара (a, a) принадлежит R, т.е. имеет место 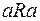для любого a из M:

.

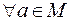
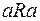Отношения «жить в одном городе», «учиться в одном вузе», «быть не больше» являются рефлексивными.

2. Бинарное отношение называется антирефлексивным, если оно не обладает свойством рефлексивности для любых a:

.

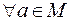
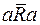Например, «быть больше», «быть младше» - это антирефлексивные отношения.

3. Бинарное отношение R называется симметричным, если для любых элементов a и b из M из того, что пара (a, b) принадлежит R, 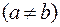, вытекает, что пара (b, a) принадлежит R, т.е.

.

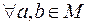
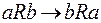
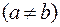Симметрична параллельность прямых, т.к. если 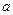//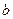, то 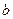//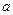. Симметрично отношение «быть равным» на любом множестве или «быть взаимнопростым на N».

Отношение R симметрично тогда и только тогда, когда R=R^-1

4. Если для несовпадающих элементов 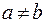верно отношение 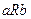, но ложно 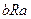, то отношение антисимметрично. Можно сказать иначе:

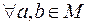
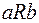и .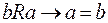

Антисимметричными являются отношения «быть больше», «быть делителем на N», «быть младше».

5. Бинарное отношение R называется транзитивным, если для любых трех элементов 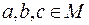из того, что пары (a, b) и (b, c) принадлежат R, следует, что пара (a, c) принадлежит R:

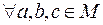
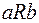и

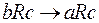
Транзитивны отношения: «быть больше», «быть параллельным», «быть равным» и др.

6. Бинарное отношение R антитранзитивно, если оно не обладает свойством транзитивности.

Например, «быть перпендикулярным» на множестве прямых плоскости (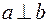, , 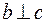но неверно, что ).

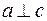Т.к. бинарное отношение может быть задано не только прямым перечислением пар, но и матрицей, то целесообразно выяснить, какими признаками характеризуется матрица отношения R, если оно: 1) рефлексивно, 2) антирефлексивно, 3)симметрично, 4) антисимметрично, 5) транзитивно.

Пусть R задано на , .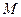

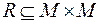1. Если R рефлексивно, то для любого 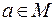имеет место 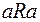, т.е. оно выполняется для всех пар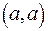 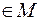. В матрице этим парам соответствуют элементы C_ii. Они составляют главную диагональ. Следовательно, главная диагональ матрицы рефлексивного отношения содержит только единицы.

2. R антирефлексивно, если ни для какого 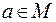не выполняется 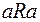. Из этого следует, что главная диагональ матрицы антирефлексивного отношения содержит только нули.

3. R симметрично, если для пары 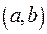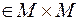из 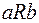следует 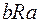, т.е. для любой пары отношение R либо выполняется в обе стороны, либо не выполняется вообще. Таким образом, если в матрице стоит единица на пересечении i - ой строки и j - ого столбца, т.е. C_ij =1, то она должна стоять и на пересечении j - ой строки и i - ого столбца, т.е. C_ji =1, и наоборот, если C_ji =1, то C_ij =1. Таким образом, матрица симметричного отношения симметрична относительно главной диагонали.

4. R антисимметрично, если из 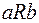и 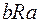следует: 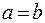. Это означает, что в соответствующей матрице ни для каких i, j не выполняется C_ij = C_ji =1. Таким образом, в матрице антисимметричного отношения отсутствуют единицы, симметричные относительно главной диагонали.

5. Бинарное отношение R на непустом множестве A называется транзитивным есл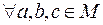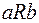и и 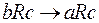. Для транзитивности отношения R необходимо и достаточно, чтобы ,

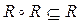Пример.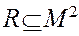

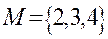
Если 2<3 и 3<4, то 2<4 Транзитивны отношения «быть параллельным», «быть больше», «быть равным».

Пример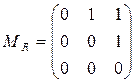

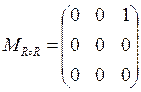
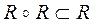, т.е. R – транзитивно

Бинарное отношение R антитранзитивно, если для любых трех элементов не выполняется условие транзитивности на множестве прямых (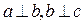, но неверно, что).

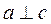Рефлексивное, транзитивное и симметричное бинарное отношение R на множестве А называется эквивалентностью на А.

Вышеприведенное условие должно выполняться для любых элементов матрицы. И, наоборот, если в матрице R имеется хотя бы один элемент C_ij =1, для которого данное условие не выполняется, то R не транзитивно.

Дата добавления: 2014-01-03