
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Парная корреляция и парная линейная регрессия
|
|
|
|
Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы. В основу таблицы положена группировка двух изучаемых во взаимосвязи признаков – X и Y. Частоты f ij показывают количество соответствующих сочетаний X и Y. Если f ij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания f ij допустимо утверждать о связи между X и Y. При этом, если f ij концентрируются около одной из двух диагоналей, имеет место прямая или обратная линейная связь.
| Уровни признака X | Уровни признака Y | |||||
| Y 1 | Y 2 | … | Ym | Итого | 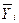
| |
| X 1 | f 11 | f 12 | … | f 1 m | 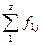
| 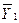
|
| X 2 | f 21 | f 22 | … | f 2 m | 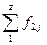
| 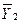
|
| … | … | … | … | … | … | … |
| X k | f k1 | f k2 | … | f k m | 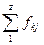
| 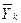
|
| Всего | 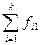
| 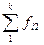
| … | 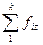
| n | 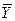
|
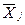
| 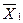
| 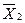
| … | 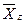
| 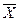
| – |
Рисунок 7.1. Схема корреляционной таблицы
Наглядным отображением корреляционной таблицы служит корреляционное поле. Оно представляет график, где на оси абсцисс откладываются значения X, по оси ординат – Y, а точками показывается сочетание первичных наблюдений X и Y. По расположению точек, их концентрации в определенном направлении можно судить о наличии и форме связи.
В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения – одно по X, другое по Y. Рассчитаем для каждого Xi среднее значение Y и для Yj среднее значение X.
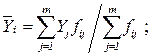
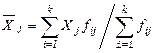 ; i = 1, 2, …, k; j = 1, 2, …, m.
; i = 1, 2, …, k; j = 1, 2, …, m.
Последовательность точек 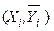 на графике иллюстрирует зависимость среднего значения результативного признака Y от факторного X; соединяя точки линиями, получаем эмпирическую линию регрессии, наглядно показывающую, как изменяется Y по мере изменения X. Аналогичным образом, последовательность точек
на графике иллюстрирует зависимость среднего значения результативного признака Y от факторного X; соединяя точки линиями, получаем эмпирическую линию регрессии, наглядно показывающую, как изменяется Y по мере изменения X. Аналогичным образом, последовательность точек 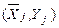 на графике иллюстрирует зависимость среднего значения факторного признака X от результативного Y; соединяя точки линиями, также получаем эмпирическую линию регрессии, наглядно показывающую, как изменяется X по мере изменения Y. Таким образом, на одном графическом поле можно расположить две линии регрессии.
на графике иллюстрирует зависимость среднего значения факторного признака X от результативного Y; соединяя точки линиями, также получаем эмпирическую линию регрессии, наглядно показывающую, как изменяется X по мере изменения Y. Таким образом, на одном графическом поле можно расположить две линии регрессии.
Пример. Ниже в корреляционной таблице представлены итоги статистического наблюдения уровня оплаты труда и производственного стажа работников.
| Стаж работы (X i), лет | Уровень оплаты (Y j), руб. | Итого | Средний уровень оплаты,
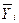 (руб.) (руб.)
| ||||
| 1500÷1750 | 1750÷2000 | 2000÷2250 | 2250 и выше | ||||
| - | - | 1708,3 | |||||
| - | 1875,0 | ||||||
| - | - | 1875,0 | |||||
| - | - | - | 2375,0 | ||||
| – | - | - | 2375,0 | ||||
| Всего | - | ||||||
Средний стаж –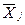 (лет) (лет)
| 0,333 | 3,25 | - | – |
На графике (рисунок 7.2) по данным таблицы показаны две эмпирические линии регрессии. Одна из них иллюстрирует изменение среднего уровня оплаты труда по мере увеличения производственного стажа (Х). Вторая линия показывает средний стаж работы при данном уровне оплаты труда (уровень Yi в серединах интервалов равен 1625, 1875, 2125 и 2375 руб.).
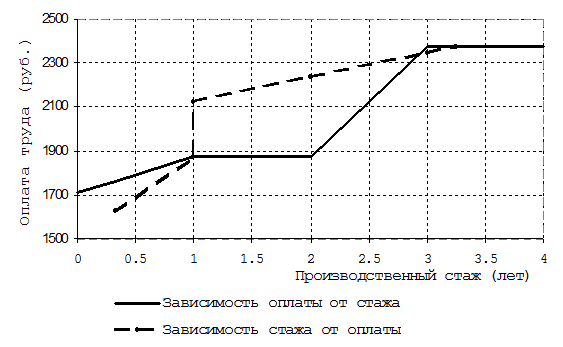
Рисунок 7.2. Эмпирические регрессии оплаты труда и стажа работы
Для количественной оценки тесноты связи в первую очередь используется линейный коэффициент корреляции (или коэффициент линейной корреляции). Корреляция переменных X и Y оценивается по формуле
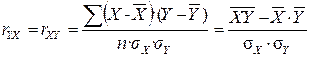 .
.
Известны и другие модификации этого выражения. Здесь n – количество наблюдений; σX, σY – соответствующие средние квадратические отклонения. Коэффициент корреляции принимает значения в интервале от –1 до +1. Принято считать, что если | r | <0,3, то связь слабая; при | r | =(0,3÷0,7) – средняя; при | г | > 0,70 – сильная или тесная. Когда | r | =1, связь функциональная. Если же r»0, то это дает основание говорить об отсутствии линейной связи между Y и X. Но в этом случае вполне возможно нелинейное взаимодействие, что требует дополнительной проверки и других измерителей (см. ниже).
Для характеристики влияния X на изменение уровня Y служат методы регрессионного анализа. В случае парной линейной зависимости строится регрессионная модель
Y i = a 0+ a 1× X i+ ei, i =1,…, n,
где i – номер наблюдения, n – число наблюдений; а 0, а 1, – неизвестные параметры уравнения регрессии; ei – случайная составляющая (ошибка) переменной Y. Собственно уравнение регрессии записывается как
Y i теор = a 0+ a 1· X i,
где Y i.теор –рассчитанное по уравнению регрессии значение результативного признака (после подстановки в уравнение числового значения Xi.). Параметры а 0 и а 1 оцениваются с помощью процедур, наибольшую известность из которых получил метод наименьших квадратов. Суть его в том, что наилучшие оценки а 0 и а 1 получают, когда
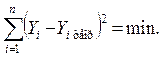
Иначе говоря, сумма квадратов отклонений фактических значений зависимой переменной Y от значений, вычисленных по уравнению регрессии должна быть минимальной. Сумма квадратов отклонений является функцией параметров а 0 и а 1. Минимальному значению суммы квадратов отклонений соответствует решение системы линейных относительно а 0 и а 1 уравнений:
n·a 0 + a 1·S X = S Y;
a 0·S X + a 1·S X 2 = S XY.
Можно воспользоваться и другими формулами, вытекающими из метода наименьших квадратов, например:
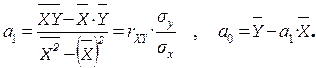
Аппарат линейной регрессии достаточно хорошо разработан и обязательно имеется в наборе стандартных программ статистического анализа на ПЭВМ. Смысл параметров: а 1 – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение X на Y. Он показывает, на сколько единиц в среднем изменится Y при изменении X на одну единицу[8]. Если а 1 больше 0, то наблюдается положительная связь. Если а 1 отрицателен, то увеличение X на единицу влечет за собой уменьшение Y в среднем на а 1. Параметр а 1 обладает размерностью отношения Y к X. Например, по данным о стоимости оборудования X и уровне производительности труда Y методом наименьших квадратов получена зависимость Y = -12,14+0,208· X. Коэффициент а 1=0,208 означает, что увеличение стоимости оборудования на 1 тыс. руб. ведет к среднему росту производительности труда на 0,208 тыс. руб. Параметр а 0 – это постоянная величина в уравнении регрессии. Его интерпретируют как начальное значение Y (или значение Y при X =0). Значения функции Y = а 0 + а 1· X на графике образуют теоретическую линию регрессии. Смысл теоретической регрессии в том, что это оценка среднего значения переменной Y для любого возможного значения X.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 764; Нарушение авторских прав?; Мы поможем в написании вашей работы!