Множественная линейная регрессия

Парная корреляция и регрессия могут рассматриваться как частный случай отражения связи некоторой зависимой переменной, с одной стороны, и одной из множества независимых переменных – с другой. Когда же требуется показать связь всего множества переменных с результативным признаком Y, говорят о множественной корреляции и о множественной регрессии. На начальных стадиях обычно используют линейные модели множественной регрессии, определяя параметры соответствующих уравнений множественной линейной регрессии.

Современные вычислительные средства позволяют за короткое время получить достаточно много вариантов уравнений множественной регрессии. Анализируя варианты, можно выбрать наилучшую линейную модель и соответствующее уравнение –

Y_i.теор= а₀ + а₁ ·X_i1 + а₂·X_i2 +... + а_k·X_ik, (i = 1, …, n),

где n – количество наблюдаемых объектов; Y_{i. теор} – расчетное значение регрессии, которое представляет собой оценку ожидаемого значения Y при фиксированных значениях переменных X _1, X ₂,..., X _k; а₁, а₂,..., а_k – параметры (коэффициенты) множественной регрессии, каждый из которых показывает, на сколько единиц изменится Y с изменением соответствующего признака X на единицу при условии, что остальные признаки останутся на прежнем уровне.

Параметры уравнения множественной линейной регрессии, как правило, находятся методом наименьших квадратов, решением системы уравнений. В матричной записи эта система имеет вид

(X^T·X)·A=X^T·Y,

где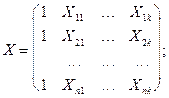

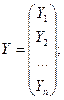
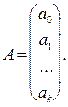
Таким образом,

.

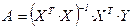Получение оценок параметров на ПЭВМ в настоящее время не представляет большой проблемы. Гораздо важнее, насколько та или иная форма связи соответствует реально существующей зависимости между Y, с одной стороны, и множеством X, с другой.

Дата добавления: 2014-01-03