Нелинейная регрессия. Коэффициенты эластичности

Представление связи линейной функцией, если в действительности имеются нелинейные соотношения, приводит к ошибкам аппроксимации и упрощенным и даже ложным положениям и выводам на основе аналитического уравнения. Вопрос о линейной или нелинейной форме уравнения регрессии следует решать на стадии теоретического анализа. На практике допускается и другая методика – нелинейность формулируется как гипотеза, очерчивается круг возможных уравнений, а затем форма и вид уравнения уточняются а процессе вычислений.

Можно выделить два класса нелинейных уравнений регрессии. К первому отнесем регрессии нелинейные относительно включенных в исследование переменных, но линейные по параметрам. Это, например, полиномы различной степени. В случае парной регрессии имеем уравнения

Y= а₀ + а₁ · X + а₂ · X² + а₃ · X³+....

Множественная полиномиальная регрессия Y = f (X ₁, X ₂) выглядит –

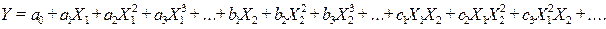
Большинство используемых на практике нелинейных парных и множественных зависимостей приводятся к линейному виду заменой переменных в формуле уравнения регрессии. Так, определяя новые переменные в предыдущей формуле, как 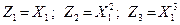и т.д., приходим к уравнению множественной линейной регрессии:

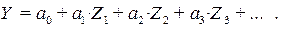
Второй класс нелинейных функций отличается нелинейностью по оцениваемым параметрам. Наиболее известна и распространена степенная функция вида

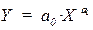для двух переменных либо

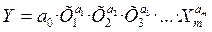для множества переменных.

Коэффициенты регрессии таких нелинейных зависимостей достаточно просто определяются, если функцию удается свести к линейной форме. Например, степенную функцию можно прологарифмировать, получив линейную зависимость Y от X в логарифмах, и применить для оценки параметров уже упоминавшийся метод наименьших квадратов[9].

Для оценки относительного влияния признака X на величину Y используют коэффициент эластичности (Э), который показывает, на сколько процентов изменится Y при изменении X на 1 процент. Расчетная формула для парной связи выглядит –

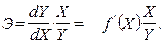
В частности, для парной степенной функции 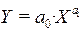коэффициент эластичности X оказывается равным параметру регрессии а ₁.

Для множественных регрессий в расчете коэффициента эластичности используется соответствующая частная производная

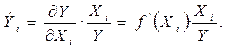
Для множественной степенной зависимости (мультипликативной модели) коэффициенты эластичности признаков Х равны соответствующим коэффициентам регрессии: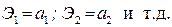

Эластичности признаков могут определяться для каждого конкретного наблюдения (объекта), но в настоящее время больше используются коэффициенты эластичности, когда в расчетную формулу подставляют среднее значение признака-результата и средние значения признаков факторных (признаков-регрессоров). Так, для множественной линейной регрессии эластичность признака X_i рассчитывается как

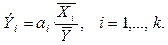
Дата добавления: 2014-01-03