Множественная корреляция. Если имеется система статистических показателей: Y, X1, X2, , Xm, то представляет интерес оценка корреляции между всеми парами показателей этой системы

Если имеется система статистических показателей: Y, X ₁, X ₂, …, X _m, то представляет интерес оценка корреляции между всеми парами показателей этой системы. Все парные коэффициенты корреляции могут быть представлены в одной квадратной матрице R размерностью (m +1) × (m +1), которая называется матрицей парных линейных коэффициентов корреляции. На основе матрицей R, можно определить так называемые коэффициенты множественной линейной корреляции признаков и коэффициенты парной линейной частной корреляции.

Коэффициент множественной линейной корреляции оценивает степень линейной связи одного из признаков системы с совокупностью прочих признаков этой же системы. В общем случае для измерения множественной линейной корреляции определяются параметры множественного уравнения регрессии и теоретические уровни признака-результата (например, Y). На основе фактических и рассчитанных по уравнению (теоретических) значений признака Y вычисляется коэффициент множественной корреляции R_y:

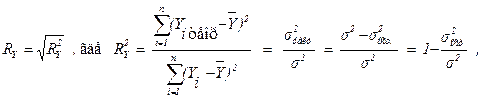
где s² – общая (фактическая) дисперсия уровней результативного признака (дисперсия Y); σ²_факт. – факторная дисперсия или дисперсия теоретических значений признака результата относительно среднего уровня; σ²_ост. – остаточная дисперсия, характеризующая вариацию Y за счет факторов, не учтенных уравнением регрессии. Известно, что общая дисперсия признака результата Y складывается из факторной и остаточной составляющих.

Коэффициент множественной корреляции изменяется от 0 до 1. Чем ближе R_Y к 1, тем более сильная связь между Y и множеством X. Если коэффициент R_Y незначителен по величине (как правило, R_Y 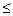0,3), то можно утверждать, что или не все важнейшие факторы взаимосвязи учтены, или выбрана неподходящая форма уравнения. В последнем случае пересматривается список переменных модели и возможно, её вид.

Для нелинейной множественной связи рассчитывают индекс корреляции. Методика его вычисления аналогична, но взаимодействие факторов и функция регрессии рассматриваются как нелинейные. Индекс корреляции изменяется в пределах от 0 до 1. Квадрат R равен так называемому коэффициенту детерминации (D или R²). Он показывает, какая часть вариации зависимого признака объясняется включенными в модель факторов.

Показатели множественной корреляции рассчитываются по приведенной выше схеме не часто. Если признак-результат Y включен в общую систему признаков, то на основе общей матрицы парных линейных коэффициентов R можно получить всю совокупность коэффициентов множественной корреляции, так как любой из признаков этой системы может, в принципе, претендовать на роль признака-результата. Коэффициент множественной корреляции, оценивающий степень линейной зависимости любого признака j от всех прочих в этой системе, определяется по формуле

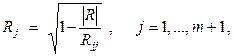
где (m +1) – число всех признаков в системе; | R | –определитель матрицы R парных линейных коэффициентов корреляции; R_ii – алгебраическое дополнение элемента (jj) для этой же матрицы.

Дата добавления: 2014-01-03