Оценка статистической значимости параметров взаимосвязи

Получив оценки параметров регрессии и корреляции, необходимо убедиться, что эти значения не случайны и действительно выражают наличие, характер и тесноту зависимости признаков. Для оценки не случайности того или иного параметра или коэффициента вводится понятие уровня значимости. Уровень значимости это, в первом приближении, вероятность того, что полученное численное значение конкретного параметра (коэффициента корреляции или параметра регрессии) можно считать величиной случайной. Таким образом, чем меньше численное значение уровня значимости, тем с большей вероятностью можно утверждать, что данный параметр является неслучайным. Для экономических задач обычно достаточно, чтобы уровень значимости был численно не более 0,05 или даже 0,10. Для статистического анализа технических систем, связанных с обеспечением жизнедеятельности, уровень значимости принимается гораздо более строгим (например, не более 0,01; 0,001 или 0,0005 и т.п.).

Системы анализа статистических данных на ЭВМ обязательно включают процедуры оценки значимости. Используют любую из двух равнозначных методик. По первой, традиционной, методике исследователь задает численную оценку уровня значимости, например α = 0,05. Под эту вероятность выбирается табличное значение t-статистики Стьюдента, если оценивается значимость параметра регрессии либо коэффициента парной линейной корреляции, или табличное значение F-статистики Фишера-Снедекора для оценки значимости уравнения регрессии в целом. Далее величина конкретного полученного параметра регрессии или коэффициента корреляции пересчитывается в фактическое значение t-статистики, а для уравнения регрессии в целом в фактическое значение F-статистики. Фактические t -статистики показывают, на сколько средних квадратических отклонений соответствующий фактический параметр регрессии или корреляции отклонился от своего гипотетического нулевого среднего уровня. Для коэффициента парной линейной корреляции и параметра а ₁ в уравнении парной регрессии фактическое значение t -статистики определяют 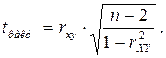Для параметра а₀: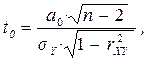

где n – количество наблюдений; r²_XY – коэффициент линейной корреляции признаков X и Y.

Для оценки значимости параметров множественной линейной регрессии: а₀, а ₁, …, а_k – соответствующие значения фактических t -статистик равны

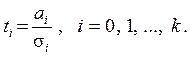
В этой формуле a_i – i -й параметр уравнения регрессии; σ_i – среднее квадратическое отклонение i -го параметра. Такая методика принята в системах статистического анализа данных на ПЭВМ.

Если фактическое значение t -статистики Стьюдента больше табличного значения (t_табл), то утверждается, что коэффициент корреляции или параметр регрессии статистически значим с уровнем, не менее α.

Согласно второй методике, определив фактическую величину t -статистики параметра регрессии, оценивают вероятность того, что за счет случайных причин эта величина могло бы быть еще большей. Если эта вероятность мала (меньше заданного численного значения уровня α), то найденный параметр признается статистически значимым. Эта методика является обычной при расчетах в системах статистического анализа данных на ПЭВМ.

При назначении табличного значения t- статистики необходимым параметром является число степеней свободы (ν). Для анализа парных линейных зависимостей число степеней свободы равно количеству наблюдений за минусом 2 (числа параметров регрессии в уравнении парной линейной связи), т.е. ν=n- 2. Для уравнений множественной линейной регрессии соответственно имеем

ν = n- (k+ 1) = n–m,

где m – количество параметров в уравнении регрессии, n – количество наблюдений, по которым составляется уравнение множественной регрессии.

Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F- критерия, определяя расчетное (фактическое) значение F- статистики. На основе квадрата коэффициента множественной корреляции (R²), числа наблюдений (n) и количества параметров в уравнении множественной линейной регрессии (m) определяем

.

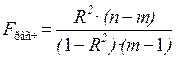Полученное по этой формуле значение F _расч также должно быть больше F _теор (табличного) при v ₁= m –1 и v ₂= n – m степенях свободы и выбранном уровне значимости α.

(Величина F-статистики показывает, во сколько раз факторная дисперсия признака результата Y превышает его остаточную дисперсию. При расчете учитываются соответствующие степени свободы).

По второй методике определяется вероятность еще большего значения F (при тех же степенях свободы v ₁= m –1 и v ₂= n – m). Эта вероятность должна быть меньше принятого числа α, иначе следует пересмотреть форму уравнения, перечень переменных и т.д.

Дата добавления: 2014-01-03