Непараметрические методы оценки связи

В методах корреляционного и регрессионного анализа взаимосвязей используются основные характеристики (параметры) распределения – средние значения и дисперсии. Эти методы получили название параметрических. Статистической наукой разработаны и такие методы, с помощью которых можно измерить связь между явлениями, не используя количественные значения признака, а, значит, и параметры распределения. Такие методы получили название непараметрических.

При оценке взаимосвязи двух качественных признаков используют представление единиц совокупности в форме так называемых таблиц взаимной сопряженности. Пример.

Занятия родителей	Число детей, занятых в	Всего
промышлен-ности строительстве	сельском хозяйстве	сфере обслужива-ния	прочих видах
1. Промышленность, строительство
2. Сельское хозяйство
3. Сфера обслуживания
4. Прочие виды деятельности
Всего

Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности. Но важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях и периодах времени. Для этого определяют, например, коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):

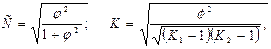
где φ² – показатель средней квадратической сопряженности, определяемый как

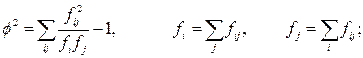
К ₁ и К ₂ – число групп по каждому из признаков; f_ij – частоты в клетках таблицы сопряженности. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, находится в обычных для этих показателей пределах от 0 до 1. Для нашего примера последовательность расчета представлена в таблице

Занятия родителей	Число детей, занятых в ло дете и, занятых < в	Всего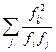
промыш ленности, строительстве	сельском хозяйстве	сфере обслуживания	прочих видах
1. Промышленность, строительство	14,04	0,56	1,11	10,71	26,42	0,2903
2. Сельское хозяйство	10.14	18,69	3,84	1,01	33,68	0,3827
3. Сфера обслуживания	2,25	0.8	5,11	2,54	10,7	0,1911
4. Прочие виды деятельности	5,05	0,56	1,84	36,51	43,96	0,3996
Итого (fj)						1,264

Цифры в верхней строке клетки перенесены из предыдущей таблицы. Цифры в центре клеток представляют результат возведения частот в квадрат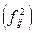.Делением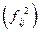 на итоговые частоты соответствующих столбцов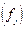получаем значения, которые записываем в нижней строке. Так, для первой клетки первого столбца 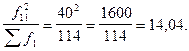Суммы этих величин по строке записываем в столбце 5. Для первой строки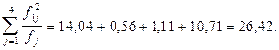

Разделим полученные суммы на итог частот по соответствующей строке (для первой строки 26,42:91=0,2903). Эти результаты записываем в последний столбец (6) расчетной таблицы. В итоге получаем:

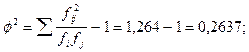
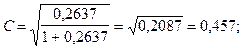
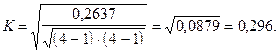
Значения коэффициентов показывают наличие заметной связи между изучаемыми признаками. Коэффициент К Чупрова обычно дает более осторожную оценку связи.

Взаимосвязь между двумя альтернативными признаками измеряется с помощью 4-х клеточных таблиц. Например,

Пол	Численность занятых
Сезонные отрасли	Несезонные отрасли	Всего
Мужчины Женщины	187 (a) 307 (c)	265 (b) 272 (d)
Всего

Доля сезонных работников среди женщин составляет 53% (307/579), среди мужчин – 41,4% (187/452). Можно утверждать, что имеется взаимосвязь признаков пола и отрасли. Оценить тесноту связи можно с помощью коэффициентов взаимной сопряженности С или К. Но проще это сделать с помощью коэффициентов контингенции или ассоциации. Используя буквенные обозначения в клетках таблицы сопряженности, коэффициент контингенции определяем по формуле

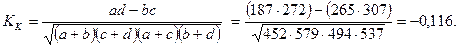
Величина коэффициента показывает наличие слабой обратной связи между анализируемыми альтернативными признаками.

Коэффициент ассоциации

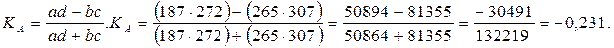Как видно, коэффициент контингенции оценивает связь более осторожно. Заметим также, что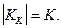

В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить, т.е. ранжировать. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д. При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Так, если 5-я и 6-я единица совокупности одинаковы, обе единицы получат ранг равный (5+6)/2=5,5. Для измерения связи между ранжированными признаками определяют ранговые коэффициенты корреляции Спирмена (r) и Кендэлла (t).

Сущность метода Спирмена в следующем:

1) располагают варианты факторного признака по возрастанию, т.е. ранжируют единицы по значению признака X;

2) для каждой единицы совокупности указывают ранг с точки зрения результативного признака Y.

Если связь прямая, то с увеличением ранга признака Х, будет возрастать и ранг Y; при тесной прямой связи ранги признаков Х и Y в основном совпадут. При обратной связи возрастанию рангов признака Х будет соответствовать общее убывание рангов признака Y. Теснота связи между признаками оценивается ранговым коэффициентом корреляции Спирмена:

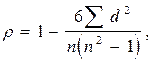
где d – разность рангов признаков Х и Y; n – число наблюдаемых единиц.

Кендэллом предложен другой показатель также с использованием рангов:

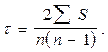
Расчет коэффициента Кендэлла выполняется в следующем порядке.

1. Ряд наблюдений располагается в возрастающем порядке по признаку Х с указанием соответствующих рангов по признаку Y.

2. Упорядоченная таким образом последовательность берется как исходная для построения квадратной матрицы (a_ij) размерностью (n×n). Далее потребуются только элементы, расположенные выше главной диагонали. По каждой паре наблюдений (i,j) сравниваем ранги признака Y:

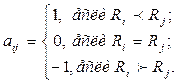
Сумма элементов a_ij, расположенных выше главной диагонали, и есть искомое значение S в формуле коэффициента Кендэлла. При некотором навыке расчет величины S можно выполнить, непосредственно сравнивая ранг Y данного наблюдения с рангами Y последующих наблюдений. Для каждого наблюдения подсчитываются Р – число случаев, когда ранг признака Y следующих наблюдений меньше, чем у данного, и Q – число случаев, когда у следующих наблюдений ранг признака Y больше, чем у данного. Искомое значение 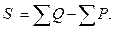Правильность вычислений контролируется соблюдением условия .

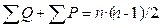Пример. Имеются данные об успеваемости 10 учащихся школы.

Учащиеся	Ранги успеваемости по наукам:	d=Rx–Ry	d^2
физико-математическим (Rx)	гуманитарным (Ry)
А Б В Г Д Е Ж И К			–2 –8 –5 –2 +1 –2 +7 +3 +8
Итого

Коэффициент Спирмена ;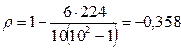

отмечена обратная, хотя и не очень сильная, связь между способностями учеников к физико-математическим и гуманитарным наукам.

Вычислим по тем же данным коэффициент Кендэлла (t). Для ученика A Q =7, Р получается при сравнении А с учениками, ранг которых по Y ниже, а по Х выше. Таких случаев 2. Всего для ученика А имеем (Q-Р)= 7-2=5. Ученика Б сравниваем со всеми следующими учениками в списке Q = 0, P = 8, Q-P=-8. По всей совокупности имеем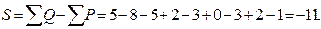

Таким образом, 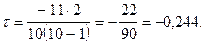Коэффициент Кендэлла также отмечает обратную, хотя и менее выраженную, связь между признаками.

Контрольные вопросы

1. Определение взаимосвязи, статистические и функциональные связи.

2. Формы и виды связей.

3. Понятие корреляционно-регрессионного анализа.

4. Множественная регрессия и корреляция.

5. Оценка значимости параметров взаимосвязи

6. Таблицы сопряженности. Коэффициенты сопряженности.

7. Коэффициенты связи для таблиц сопряженности 2х2.

8. Ранговая корреляция.

Дата добавления: 2014-01-03