Общие индексы и их применение в анализе

Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, анализ выполняют посредством так называемых общих индексов. Индекс выступает как общий, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например:

Q = Sр ∙ q.

Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так, например, получают индекс динамики общего объема товарооборота в агрегатной форме:

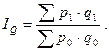
Прирост товарооборота объясняется изменением уровня цен и количества проданных товаров. Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен I_p, который в предположении первичности изменения количественного показателя (q) и вторичности – качественного (р) имеет вид

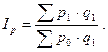
Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема I_q, который строится также в предположении первичности изменения количественных показателей (q) и вторичности влияния качественных (р):

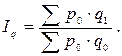
В форме мультипликативной индексной модели динамика товарооборота будет выражаться соотношениями

I_Q = I_q · I_p или Q₁ = Q₀ · I_q · I_p,

где Q ₀ = Sp ₀ ·q ₀; Q ₁ = Sp ₁· q ₁.

Общий прирост товарооборота будет распределяться по факторам следующим образом: DQ(q) = Q ₀·(I_q- 1); DQ(p) = Q₀ ∙ I_q ∙ (I_р - 1 ).

Если же принимается предположение об обратной последовательности влияния факторов – сначала р, затем q, то меняются и формулы разложения прироста и формулы расчета индексов I_q и I_р. Тогда

DQ(q) = Q ₀∙ I_p ∙ (I_q – 1 );

DQ(p) = Q ₀∙ (I_р – 1 ).

где I_p = (S p ₁∙ q ₀)/(S p ₀∙ q ₀); I_q = (S p ₁∙ q ₀)/(S p ₀∙ q ₀).

(Отдельные слагаемые общего изменения итогового показателя можно, в принципе, получить и как разности числителя и знаменателя в формулах соответствующих агрегатных индексов).

Примером мультипликативной индексной модели с большим числом факторов является изменение общей суммы материальных затрат на производство продукции. Сумма затрат зависит от количества выпущенной продукции (индекс I_q), удельных расходов (норм) материала на единицу продукции (индекс I_n) и цены на материалы (индекс I_р). Прирост общей суммы затрат распределяется следующим образом:

DM(q) = M₀·(I_q – 1 );

DМ(n)=М₀·I_q·(I_n – 1 );

DМ(р)=М₀·I_q·I_n ·(I_p – 1 ).

где М₀ = Sq ₀ ·n ₀ ·р₀, а величины индексов таковы:

индекс увеличения суммы затрат в связи с изменением объемов производства продукции (индекс физического объема)

;

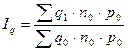индекс изменения суммы затрат за счет изменения удельных расходов материала (индекс удельных расходов)

;

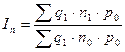индекс изменения общей суммы затрат, объясняемого изменением цен на материалы (индекс цен на материалы)

.

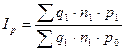Приведем формулы некоторых агрегатных индексов наиболее употребляемых в экономическом анализе.

Индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства (q) и затрат на единицу (z):

.

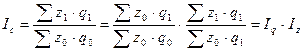Индекс изменения фонда оплаты труда в связи с изменением общей численности персонада (Т) и заработной платы (f):

.

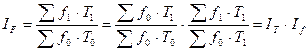Индекс изменения объема продукции в связи с изменением численности работающих (Т) и уровня их выработки (w):

.

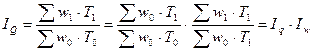Индекс изменения объема продукции в связи с изменением объема основных производственных фондов (Ф) и показателя эффективности их использования – фондоотдачи (Н).

.

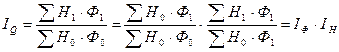Аналогичным образом находят общие агрегатные индексы и по многим другим экономическим показателям. Используемые в приведенных формулах индексы I_q, I_Т, I_Ф получаются по методу индекса физического объема, а индексы I_z, I_f, I_w, I_H, – по методу индекса цен. Таким образом, рассмотренная выше методика полностью приложима к анализу прироста продукции, изменения общих затрат на производство, изменения общего фонда оплаты труда и т.д.

Отметим, что для распределения прироста итогового показателя по нескольким факторам динамики предварительно задается последовательность, очередность соответствующих индексов в мультипликативной индексной модели. В классической схеме индексного анализа предполагается последовательное изменение итогового показателя сначала за счет сугубо количественного, а затем за счет все более и более качественных факторов. При отсутствии информации о фактической динамике явления, когда и индексы, и величина итогового признака становятся известными лишь по конечному результату всего периода, любая последовательность влияния факторов в мультипликативной индексной схеме оказывается равновероятной; исследователь вправе выбрать для анализа любую в наибольшей степени отражающую реальность схему очередности факторов. В условиях же полной неопределенности следует ориентироваться на так называемые равновероятностные схемы индексного анализа. Рассмотрение их выходит за пределы данного курса.

9.3. Общий индекс как средняя величина
индивидуальных индексов

Общий индекс можно получить как среднее значение соответствующих индивидуальных индексов. В этом смысле общим индексом отражаются результаты изменения уровня явления у отдельных единиц совокупности. При расчете общего индекса как средней величины веса индивидуальных индексов подбираются так, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме[14]. Эти преобразования, как правило, не сложны. Например, индекс общего объема товарооборота можно представить средней арифметической величиной -

.

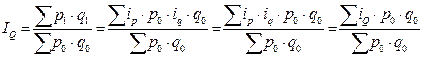Тот же индекс может быть записан в форме средней гармонической величины.

.

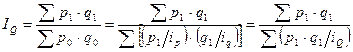Индекс изменения общей суммы товарооборота в связи с изменением количества проданных товаров (индекс физического объема – I_q) можно представить как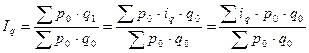

(В форме средней гармонической индекс физического объема практически не используется).

Индекс изменения общей суммы товарооборота в связи с изменением цен на товары (I_p) можно представить средней гармонической величиной:

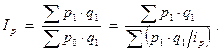
9.4. Индексный метод анализа итогового показателя
и структурных изменений

Показанные выше общие индексы в агрегатной форме либо в форме средней величины позволяют оценить вклад отдельных факторов (например, изменение объема продаж и цены товаров, объема кредитных услуг и процентной ставки и т.п.) в общий прирост итогового показателя. Методика индексного анализа изменения итогового показателя (изменения общей суммы выручки от реализации, прироста общей суммы дохода от предоставления кредитных услуг разного типа и т.д.) применима при анализе совокупностей, состоящих как из разных объектов, так и из объектов одного и того же типа.

Если совокупность неоднородна (например, совокупность товаров различного вида), то индекс физического объема – единственный способ показать динамику такой массы различных предметов, выражая ее через взвешивающий множитель (цену, себестоимость, трудоемкость), а агрегатный индекс качественного показателя, например, агрегатный индекс цен – это единственный способ оценить общее изменение уровня качественного признака, например, общее изменение цен.

Если же совокупность состоит из объектов одного типа, то динамику этой массы можно показать непосредственным сравнением общего количества таких предметов в отчетном периоде с аналогичным значением в базисном периоде. Так, при анализе изменения валового дохода банка можно определить индекс общего объема кредитных услуг как отношение суммы кредитных услуг банка (объема среднегодовой задолженности) в отчетном периоде к соответствующей сумме в базисном периоде –

I_SK = SK₁ / SK₀,

а также индекс физического объема кредитных услуг, показывающий, во сколько раз изменилась общая сумма дохода банка за счет изменения объема по отдельным видам предоставляемого кредита –

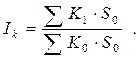
Рассмотрим пример движения валового дохода коммерческого банка в зависимости от изменения среднегодовой задолженности по кредитам (количественный фактор – K) и процентной ставки за кредит (качественный фактор – S). Исходные данные приведены в таблице

Виды кредитов	Базисный период	Отчетный период
Среднегодовая задолженность (K0 ), млн. руб.	Средняя процентная ставка (S0), %	Среднегодовая задолженность (K0), млн. руб.	Средняя процентная ставка (S0), %
1. Краткосрочные	665,5	4,7032306	702,0	4,8290598
2. Долгосрочные	169,5	1,7286135	298,0	1,8020134
Итого	835,0	4,0994011	1000,0	3,927

Валовой доход от реализации кредита составлял:

в базисном году – ВД0 = SК0·S0 = 34,23 млн. руб.,

в отчетном году - ВД1 =SК1·S1 = 39,27 млн. руб.

Прирост валового дохода (ВД1 - ВД0) = 5,04 млн. руб.

Условная величина дохода от предоставления кредитных услуг в отчетном периоде при базисной процентной ставке была бы равна SК1·S0 = 38,168 млн. руб.

Индекс общего объема кредитных услуг равен

ISK = SK1 / SK0 = 1000/835 = 1,1976047.

Индекс физического объема кредитных услуг равен

.

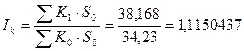Индекс изменения величины процентной ставки за кредит равен

.

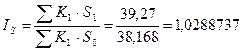Таким образом, прирост валового дохода объясняется

а) изменением объема кредитных услуг DД(К) = 34,230–(1,1150437–1) = 3,938 млн. руб.;

б) изменением процентной ставки DД(S) = 34,230–1,1150437–(1,0288737–1) = 1,102 млн. руб.

Более детальный анализ изменения итогового показателя возможен при изучении так называемых структурных сдвигов и их влияния на прирост итогового показателя (продукции, валового дохода, общих затрат на производство и т.д.).

Рассмотрим соотношение между индексами физического объема (I_K) и общего объема (I_SK). В формуле I_K разделим и умножим числитель на SK₁ а знаменатель – на SK₀. Получим

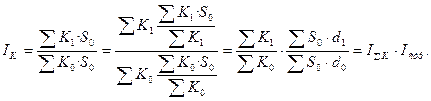
Таким образом, для однородных совокупностей (допускающих суммирование по количественному признаку) индекс физического объема есть произведение индекса общего объема совокупности на индекс, выражающий изменение структуры совокупности (в данном случае – это изменение удельного веса отдельных видов кредитных услуг в общей их сумме).

Формула индекса структурных изменений для нашего примера:

,

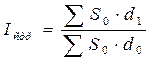где d ₀ – удельные веса, доли отдельных видов кредитных услуг в общем их объеме в базисном периоде, а d ₁ – удельные веса или доли отдельных видов кредитных услуг в общем их объеме в отчетном периоде:

d ₀ = K ₀ / SK ₀, d ₁ = K ₁ / SK ₁.

Знаменатель в формуле индекса структурных изменений в нашем примере есть не что иное, как средний размер процентной ставки по всем видам кредитов в базисном периоде, так как .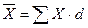

Экономическая сущность индекса структурных изменений в том, что он показывает влияние процессов перераспределения на общий прирост итогового показателя. В той же мере этот индекс показывает, во сколько раз изменился общий средний уровень качественного показателя (средней процентной ставки, средней цены, среднего уровня оплаты труда и т.п.) только за счет изменения удельного веса каждого объекта в общем объеме количественного признака.

При известных значениях I_K и I_SK, влияние структурных сдвигов на средний уровень процентной ставки и на общий дохода банка определяется просто: I_стр = I_K /I_SK. В примере I_стр= I_K /I_SK. = 1,1150437/1,1976047 = 0,9310615.

Для непосредственного расчета I_стр следует определить долю каждого вида кредитных услуг в базисном (d₀) и в отчетном (d₁) периодах и использовать формулу I_стр:

Виды кредита	d 0	d 1	S 0
1. Краткосрочные	0,797006	0,702	4,7032306
2. Долгосрочные	0,202994	0,298	1,7286135

Отсюда

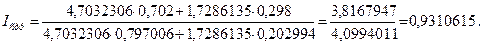
Таким образом, прирост валового дохода банка происходил за счет:

1) изменения объема задолженности (объема кредитных услуг)

DД(SК) = Д₀ (I_SK – 1 ) = 34,23 (1,1976047 – 1 ) = +6,764 млн. руб.;

2) перераспределения задолженности по разным формам кредита

DД_стр = Д₀ · I_SK · (I_стр – 1 ) = 34,23∙1,1976047∙(0,9310615–1) = –2,826 млн. руб.;

3) изменения процентной ставки за кредит

DД(S) = Д₀ · I_SK · I_стр · (I_S – 1 ) = 1,102 млн. руб.

Вклад разных факторов в общий прирост можно распределить по отдельным объектам совокупности, для каждого из которых применяют мультипликативную индексную модель

q ₁ = q ₀ · I_SK ∙ i_d ∙ i_s, ∙

где q0, q1 – объемы итогового признака (дохода) по данному объекту (виду услуг);

I_SK – общий для всей совокупности индекс количественного признака; is – индивидуальный для данного объекта индекс изменения уровня качественного признака;

i_d – индивидуальный индекс доли данного объекта в общем объеме количественного признака.

Распределение общего прироста валового дохода по видам кредитных услуг и по факторам в окончательном виде выглядит:

Вид кредита	Прирост валового дохода банка за счет:	Всего
изменения объема задолженности	перераспределения задолженности по видам кредита	изменения процентной ставки
Краткосрочный	6,185	–4,468	0,883	2,60
Долгосрочный	0,579	1,642	0,219	2,44
Итого	6,764	–2,826	1,102	5,04

Дата добавления: 2014-01-03