Геометрический смысл дифференциала

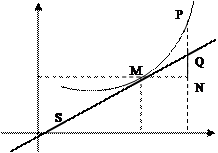Рассмотрим график функции y = f(x). Пусть точка М на кривой соответствует значению аргумента x, точка Р на ой же кривой соответствует значению аргумента x + Dx, МS – касательная к кривой y = f(x) в точке М. Пусть, далее, прямая MN параллельна Ox, прямая PN параллельна Oy, Q – точка пересечения касательной MS с прямой PN. Тогда приращение Dy равно величине отрезка NP. В то же время из прямоугольного треугольника MQN и из формулы 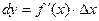ясно, что дифференциал функции dy равен величине отрезка NQ, ибо величина отрезка MN равна Dx, а тангенс угла Ð QMN равен f¢(x). Очевидно, что величины отрезков NP и NQ, вообще говоря, различны.

Таким образом, мы получили, что дифференциал 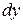функции равен произведению ее производной и дифференциала независимой переменной:

.

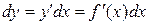Пример 1. Найти дифференциал функции .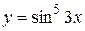

Решение: найдем производную данной функции:

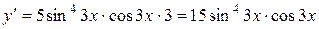, тогда

.

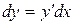
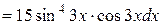Так как дифференциал функции отличается от ее приращения на бесконечно малую высшего порядка по сравнению с величиной dx, то 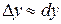, или 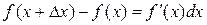, откуда получаем

.

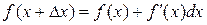Полученная формула часто применяется для приближенного вычисления значений функции при малом приращении D х независимой переменной х.

Пример 2. Вычислить приращение стороны куба, если его объем увеличится от 27 до 27,1 м ³.

Решение: если х – объем куба, то его сторона 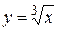. По условию задачи х = 27, D х = 0,1. Тогда приращение стороны куба

.

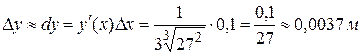Пример 3. Найти приближенно .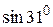

Решение: Полагаем х = 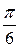, тогда ,

.

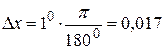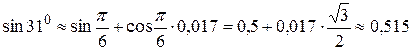С помощью дифференциала функции вычисляют абсолютную погрешность функции e_у, если известна абсолютная погрешность e_х аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.

Пусть требуется вычислить значение функции y = f(x) при некотором значении аргумента х, истинная величина которого нам известна, но дано его приближенное значение х₀ с абсолютной погрешностью e_х:

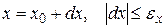. Тогда 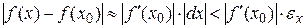. Отсюда видно, что .

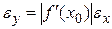Относительная погрешность функции d_у выражается формулой

.

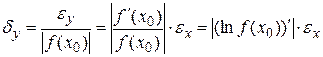Например, если в предыдущем примере принять e_х = 0,017, то

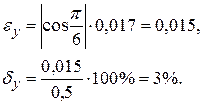
Рассмотрим теперь методы исследования функций и построение их графиков, которые широко используются как в теории и на практике.

Теорема 1. (теорема Ферма, Пьер Ферма (1601-1655) – французский математик).

Пусть функция f(x) определена на интервале 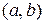и в некоторой точке х₀ этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке х₀ существует производная, то она равна нулю, т.е. .

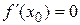Доказательство. Пусть функция f(x) в точке х₀ имеет наибольшее значение, т.е. 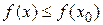для любого хÎ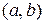. Это означает, что Dу £ 0 для любой точки х₀+DхÎ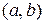. Поэтому, если Dх > 0 (х > х₀), то Dу/Dх £ 0 и, следовательно,

,

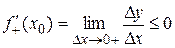если же Dх < 0 (х < х₀), то Dу/Dх ³ 0 и, следовательно,

,

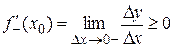т.е. правая производная в точке х₀ неположительная, а левая – неотрицательная. По условию, 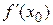существует и, значит, 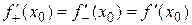. Это возможно только в случае, когда 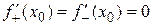. Но тогда и .

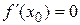Аналогично рассматривается случай, когда в точке х₀ функция f(x) имеет наименьшее значение. (ч.т.д.)

Геометрический смысл теоремы Ферма состоит в том, что если в точке х₀ дифференцируемая функция имеет наибольшее или наименьшее значение, то в точке (x₀, f(x₀)) касательная к графику функции f(x) параллельна оси Ох.

Теорема 2. (теорема Роля (Роль Мишель(1652-1719) – французский математик). Пусть на 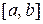определена функция f(x), причем:

1) f(x) непрерывна на ;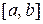

2) f(x) дифференцируема на ;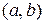

3) .

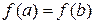Тогда существует точка с Î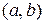, в которой .

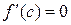Геометрически теорема Роля означает, что у графика непрерывной на отрезке и дифференцируемой внутри этого отрезка функции, принимающей на его концах равные значения, существует точка 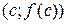, в которой касательная параллельна оси Ох.

Теорема 3. (теорема Лагранжа, Жозеф-Луи Лагранж(1736-1813) – французский математик).

Пусть на 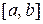определена функция f(x), причем:

1) f(x) непрерывна на ;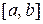

2) f(x) дифференцируема на ;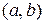

Тогда существует точка с Î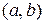такая, что справедлива формула

.

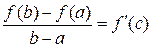Установим геометрический смысл теоремы Лагранжа.

Величина 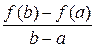является угловым коэффициентом секущей, проходящей через точк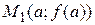и и 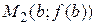графика функции 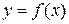, а 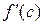- угловой коэффициент касательной к к графику в точке 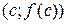. Из теоремы Лагранжа следует, что существует точка с такая, что касательная к графику в точке 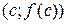параллельна секущей М₁М₂. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.

Замечание 1. Равенство 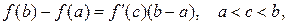называется формулой Лагранжа или формулой конечных приращений.

Замечание 2. Если положить 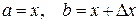, то получим 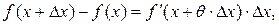где .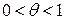

Теорема 4. (теорема Коши, Коши Огюстен Луи (1789-1857) – французский математик).

Пусть функции f(x) и g(x), непрерывны на 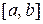и дифференцируемы на 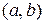. Пусть, кроме того, 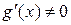. Тогда существует точка с Î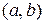такая, что справедлива формула

.

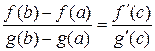Эта формула называется формулой Коши или обобщенной формулой конечных приращений.

Дата добавления: 2014-01-03