Формулы Тейлора и Маклорена

Лекция 6. Применение дифференциального исчисления.

Рассмотрим одну из главных формул математического анализа, имеющую многочисленные применения как в самом анализе, так и в смежных дисциплинах.

Теорема Тейлора (Брук Тейлор (1685-1731) – английский математик).

Пусть функция f(x) имеет в точке 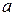и некоторой ее окрестности производные порядка n + 1. Пусть х – любое значение аргумента из указанной окрестности, х ¹ 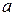. Тогда между точками 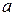и х найдется точка x такая, что справедлива следующая формула:

.

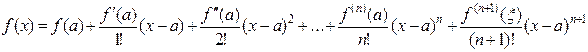Эта формула называется формулой Тейлора, а выражение 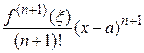, которое обозначается 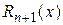, называется остаточным членом в форме Лагранжа. Его можно переписать в другом виде. Так как точка 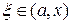, то найдется такое число 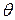из интервала 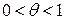, что 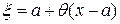, и остаточный член примет вид

.

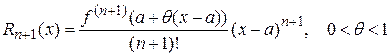Часто формулу Тейлора записывают в ином виде. Положив 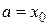, , 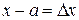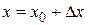. Тогда:

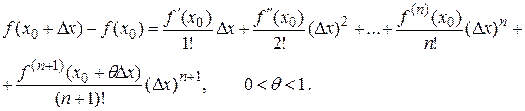
При 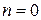из этой формулы получается формула Лагранжа

.

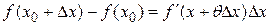Если функция 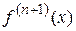ограничена в окрестности точки 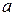, то остаточный член 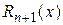является бесконечно малой более высокого порядка, чем 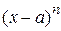при :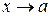

,

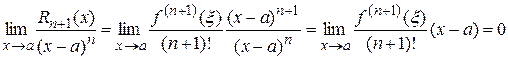Таким образом, 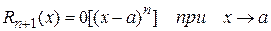. Эта формула называется остаточным членом в форме Пеано (Джузеппе Пеано (1858-1932) – итальянский математик).

Формулой Маклорена называют формулу Тейлора при :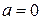

.

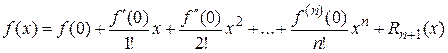Остаточный член имеет вид:

в форме Лагранжа ;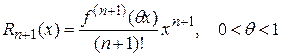

в форме Пеано .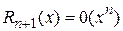

Формула Маклорена применяется для представления некоторых элементарных функций в виде многочлена. Приведем некоторые примеры.

1) Рассмотрим функцию 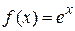. Так как

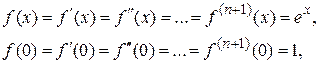
то по формуле Маклорена данная функция имеет вид

.

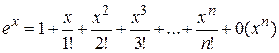2) Рассмотрим функцию 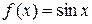. Вычисляя производные и их значения при х = 0, получим

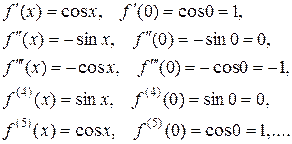
Или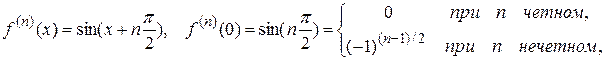

Значит данная функция по формуле Маклорена имеет вид

.

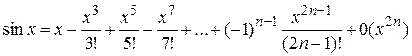3) Рассмотрим функцию 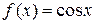. Вычисляя производные и их значения при х = 0, получим:

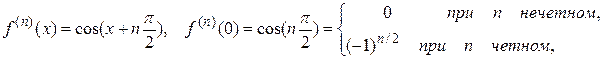
Данная функция по формуле Маклорена имеет вид

.

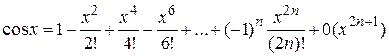В этой формуле остаточный член записан в виде 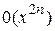, а не в виде 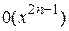, так как следующий за последним член равен нулю (тоже самое относится и к предыдущей формуле).

4) Рассмотрим функцию 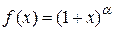, где 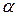- вещественное число. Так как

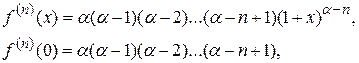
то по формуле Маклорена данная функция имеет вид

,

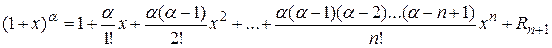В частном случае, когда 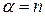- натуральное число, 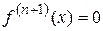, следовательно, 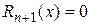, мы получаем известную из элементарной математики формулу бинома Ньютона

.

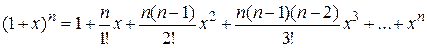Эти примеры показывают, что функции можно представлять в виде многочленов. Над многочленами удобно выполнять арифметические действия, нетрудно вычислить значение многочлена в любой точке и т.д. Формулы Тейлора и Маклорена позволяют приближенно заменять многочленами и более сложные функции.

Формула Тейлора является эффективным средством для вычисления пределов функций, с которыми часто приходится иметь дело при исследовании функций.

Пример 1. Найти .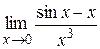

Решение. По формуле 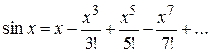, при имеем

==.

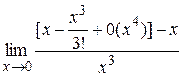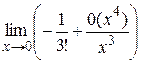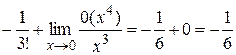Пример 2. Найти .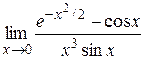

Решение. Используя формулы, заменяем три функции

==

====.

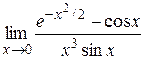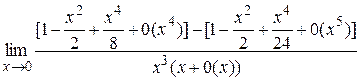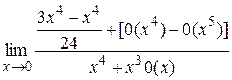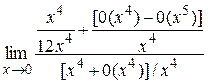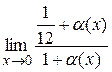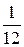Дата добавления: 2014-01-03