Уравнения движения

Классификация сплошных сред

жидкости s_ij = - P_ii g_ij + τ_ij

Здесь g_ij – метрический тензор (единичный тензор для прямоугольной декартовой системы координат), P_ii - давление, τ_ij - тензор сдвиговых напряжений.

Ньютоновская жидкость τ_ij = 2η e_ij

η – коэффициент динамической вязкости

коэффициент кинематической вязкости 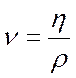, где 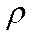- плотность жидкости.

Рассмотрим одномерное течение Куэтта - в плоскости 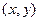происходит течение, при котором скорости частиц жидкости направлены вдоль оси 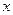и пропорциональны координате .

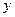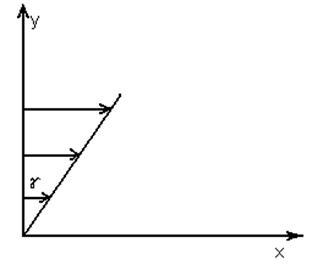
Деформация будет деформацией чистого сдвига. Здесь γ – угол сдвига, dγ/dt – скорость сдвига.

Тензор деформации будет равен

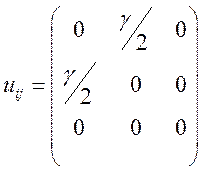
Тогда тензор скоростей деформации будет равен

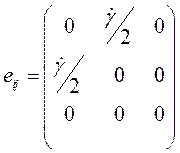
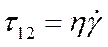
Для одномерного течения Куэтта обозначают также τ = η dγ/dt

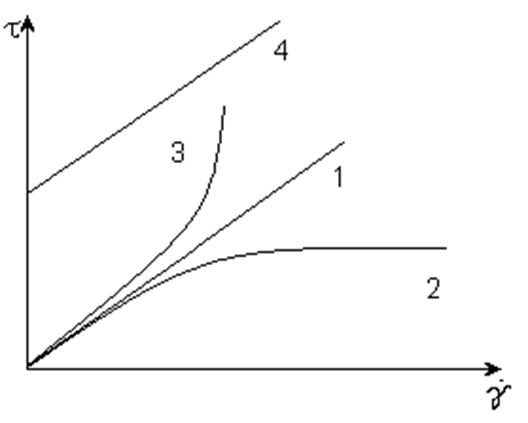
Ньютоновские и Неньютоновские жидкости:

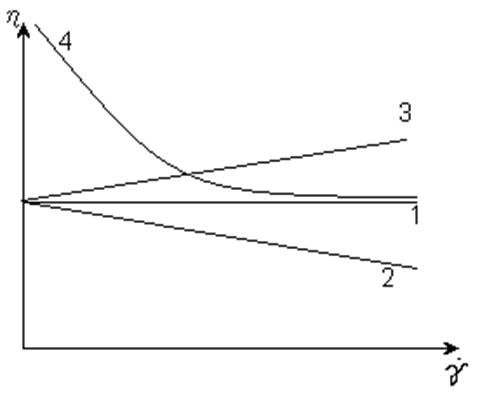
1- ньютоновская

2- псевдопластическая жидкость – снижение кажущейся вязкости из-за распада частиц и др. явлений.

3- дилатантная жидкость – дезориентация частиц потоком, сухое трение

4- Вязкопластическая жидкость (вязкопластическое тело): модель Шведова-Бингама

dγ/dt = 0, если τ < τ₀

τ = η dγ/dt + τ₀, если τ > τ₀

Лучше говорить о характере течения (вязкопластическое, псевдопластическое, дилатантное)

Графики для напряжения сдвига и кажущейся вязкости

2.4. Уравнения (законы сохранения) для многофазной и/или многокомпонентной сплошной среды

Уравнения баланса массы и импульса

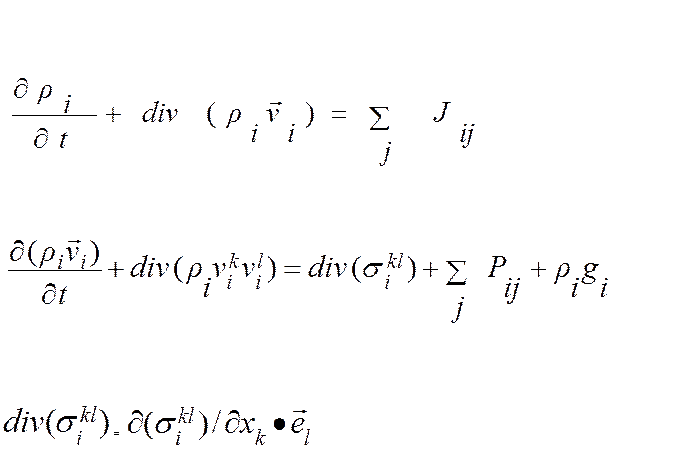
+ уравнения баланса энергии, момента импульса

+ определяющие соотношения для потоков тепла, массы

+ реологические соотношения, связывающие тензоры напряжений и деформаций

Мягкие ткани: основные тензорные уравнения и свойства

1. Анизотропия

Для линейно-упругого анизотропного тела

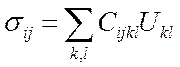Всего 3⁴ = 81 коэффициент 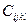, из них 21 коэффициент независимый.

Энергия деформации

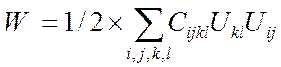
У изотропного тела есть только две упругие константы.

Тело Гука

σ_ij = Ku_kk δ_ij + 2μ(u_ij – 1/3 δ_iju_kk)

Дата добавления: 2014-01-03