Вязкость газов. Эмпирическое уравнение переноса Ньютона

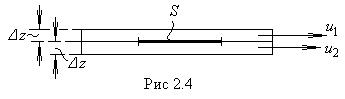
Чтобы понять происхождение силы внутреннего трения, рассмотрим два соприкасающихся слоя газа некоторой толщины ∆z. Пред­положим, что слои движутся с различными скоростям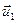и и 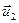(рис.2.4). Каждая молекула газа участвует в двух движениях: хаотическом тепловом, сред­няя скорость которого равна 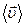, и упорядоченном движе­нии со скоростью 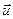, которая много меньше, чем .

Пусть в какой-то момент времени слои обладают им­пульсам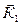и и 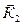. Эти импульсы не могут оставаться неизменными, так как вследствие теплового движения происходит непрерывный переход молекул из одного слоя в другой. Будем считать, что тепловое движение моле­кул происходит вдоль трех взаимно перпендикулярных направ­лений. За время ∆ t через поверхность S переходит в обоих направлениях одинаковое количество молекул, равное

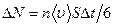. (2.1)

Попав в другой слой, молекула претерпевает соударения с моле­кулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движу­щегося с большей скоростью), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося с меньшей скоростью). В итоге импульс более быстро движущегося слоя убывает, а более медленно движущегося — возрастает.

Например, из первого слоя уносится молекулами за время ∆ t импульс, равный

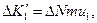
где ∆ N определяется формулой (2.1), m — масса молекулы. Одно­временно в этот слой привносится импульс

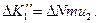
Следовательно, за время ∆ t импульс первого слоя получает прира­щение, равное

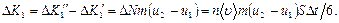
Аналогично, импульс второго слоя получает при этом приращение

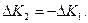
Количество какой-либо величины (энергии, импульса, частиц, массы и т. п.), проходящее в единицу времени через некоторую по­верхность S, называется потоком этой величины через поверх­ность.

Поток есть алгебраическая величина: если, например, импульс передается в положительном направлении оси z, поток К положи­телен; если же импульс передается в отрицательном направлении оси z, поток К отрицателен.

Таким образом, тепловое движение молекул приводит к тому, что через поверхность соприкосновения слоев возникает поток импульса К, равный

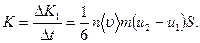(2.2)

Это эмпирическое уравнение переноса Ньютона.

Основываясь на связи между изменением импульса и силой, можно утверждать, что движение слоев происходит таким образом, как если бы по поверхности S на первый слой действовала сила

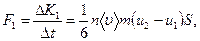
а на второй слой — сила 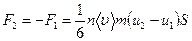(имеются в виду проекции сил 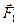и 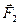на направление движения слоев).

Чтобы получить окончательную формулу для потока импульса, нужно честь, что скорость не может изме­няться скачком на границе двух слоев, а изменяется непрерывно в перпендикулярном к слоям направлении z (u = u (z), рис.2.5). Каждая молекула, пролетающая через поверхность S, переносит импульс, определяемый значением скорости u в том месте, где произошло последнее столкновение молекулы. Через поверх­ность S будут пролетать молекулы, претерпевшие соударение на са­мых различных расстояниях 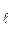от S.

Найдем средний запас импульса 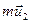, с которым молекулы пере­секают поверхность раздела слоев, двигаясь в направлении оси z (рис.2.5). Импульс, который несет молекула, претерпевшая соударение на расстоянии 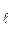от S, можно записать в виде

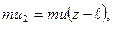(2.3)

где z — координата плоскости S.

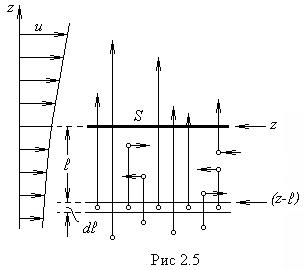Рассмотрим те молекулы, которые, претерпев соударение в слое толщины 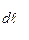, находящемся на расстоянии 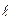от S, пролетают затем без столкновений путь 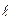и по­падают в область, лежа­щую за поверхностью S (рис.2.5). Эти молекулы переносят через S импульс, определяемый формулой (2.3). События, заклю­чающиеся в столкновении в слое 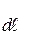и пролете без столкновений пути 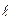, явля­ются статистически незави­симыми. Вероятность пер­вого события равна 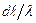, ве­роятность второго события 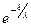. Следовательно, вероятность 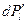того, что молекулы испытают соударение в слое 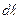и пролетят затем через поверхность S, не испытав на пути 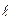соударений, равна произве­дению указанных вероятностей:

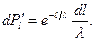(2.4)

Одновременно выражение (2.4) будет определять вероятность того, что молекула, пересекающая, поверхность S, несет с собой импульс (2.3). Среднее значение импульса, переносимого молекулой через поверхность S, равно

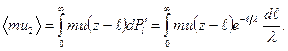(2.5)

Из-за быстрого убывания экспоненты основной вклад в интеграл вносит интервал от 0 до 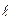порядка нескольких 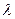. Вследствие малости 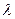функцию u (z – 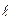) можно в пределах этого интервала представить в виде

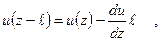
где du / dz — значение производной в точке z. Подстановка этого выражения в (2.5) дает

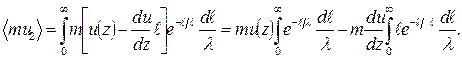
Первый интеграл в получившемся выражении равен единице, второй интеграл дает 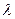. Таким образом,

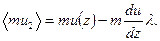(2.6)

Аналогичные выкладки приводят для молекул, летящих в на­правлении, противоположном направлению оси z, к среднему значе­нию импульса, равному

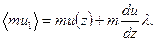(2.7)

Теперь поток импульса можно вычислить по формуле (2.2), подставив вместо mu ₁ и mu ₂ значения (2.7) и (2.6). В результате получим

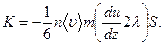
Приняв во внимание, что nm равно плотности газа ρ, последнюю формулу можно написать в виде

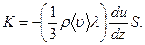
Коэффициент пропорциональности 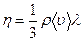называют коэффициентом вязкости газов. Заменив ρ на nm и учтя, что 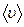пропорцио­нальна 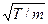, а λ обратно пропорциональна n σ, можно написать:

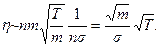
Мы получили, что η не зависит от числа молекул в единице объема, а следовательно, и от давления (р = nkT). Этот результат имеет следующее объяснение. С понижением давления уменьшается n, т. е. число молекул, участвующих в переносе импульса. Одновре­менно растет λ, а значит, и различие в импульсах, переносимых одной молекулой в противоположных направлениях. В итоге полу­чается, что суммарный импульс, переносимый молекулами при дан­ном градиенте скорости du / dz, не зависит от давления. Это справед­ливо лишь до тех пор, пока λ остается малой по сравнению с разме­рами зазора, в котором течет газ (например, по сравнению с диа­метром трубы). По мере того как перестает выполняться это усло­вие, вязкость начинает все больше зависеть от давления, уменьшаясь с его понижением. Когда средняя длина пробега становится сравни­мой с размерами зазора, в котором течет газ, пробег молекул будет определяться величиной зазора и λ перестает зависеть от давления. Число же молекул в единице объема при уменьшении давления про­должает убывать, вследствие чего уменьшается и η.

Очевидно, коэффициент вязкости должен расти с темпера­турой пропорционально 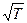. Опыт дает, что η возрастает несколько быстрее, чем 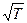. Причиной этого служит зависимость средней длины свободного пробега от температуры.

Дата добавления: 2014-01-03