
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение угла наклона плоскости к плоскости проекций
|
|
|
|
Проекции плоскостей
Лекция №3 (3-я неделя)
Конспект лекций
Лектор потока: Зелёв Александр Павлович (доцент кафедры начертательной геометрии и черчения).
Постановка задачи. Дана плоскость общего положения Г. Требуется определить углы наклона плоскости Г к плоскостям проекций (отдельно к плоскости П1, к плоскости П2, к плоскости П3).
Пусть плоскость задана треугольником Г(АВС):
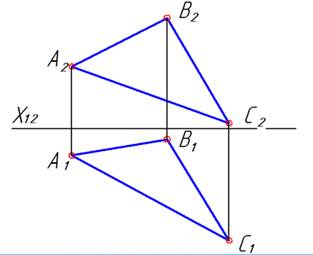
| |
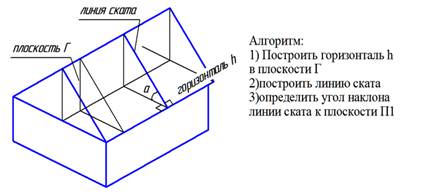
| Для изучения алгоритма рассмотрим известный геометрический объект – плоскость крыши дома. В этой плоскости построим горизонталь (кромка крыши). Построим еще одну прямую – линию ската, по которой скатывается материальная точка. Линия ската – прямая, принадлежащая исследуемой плоскости общего положения и принадлежащая данной плоскости. Из школьной программы: углом между двумя плоскостями является угол между прямыми в данных плоскостях, перпендикулярными к линии пересечения. В рассматриваемом случае проведем через горизонталь плоскость уровня, параллельную П1. Тогда углом между плоскостью крыши и горизонтальной плоскостью будет угол между линией ската и ее горизонтальной проекцией. | |
| |
| Возвращаемся к комплексному чертежу. По этому алгоритму через любую точку плоскости Г построим горизонталь в плоскости Г. Например, через точку А. Построение начинаем с фронтальной проекции (горизонталь параллельна П1) | 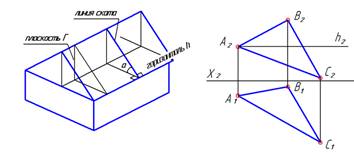
|
| «Привязываем» ее к плоскости Г с помощью точки на ВС. | 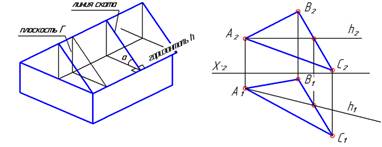
|
| Строим проекции линии ската. Таких линий – бесчисленное множество. Построим, например, через точку В. Используем проекционные свойства прямого угла. Так как линия ската перпендикулярна горизонтали, то на П1 линия ската m1 должна быть перпендикулярна h1. | 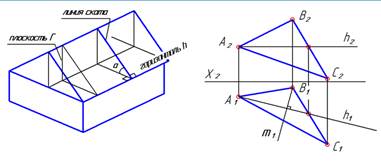
|
| Линия ската принадлежит плоскости Г. Поэтому ее «привязываем» к плоскости Г с помощью точек этой плоскости. Здесь применили точки В и К. Таким образом, построили две проекции линии ската m. | 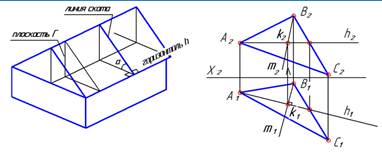
|
| Далее, надо определить угол наклона линии ската m к плоскости проекций П1. Возьмем любой отрезок на линии ската и с помощью способа прямоугольного треугольника определим этот угол. Для удобства построения используем отрезок ВК, так как в точке К уже построен прямой угол. Искомый угол – угол a. | 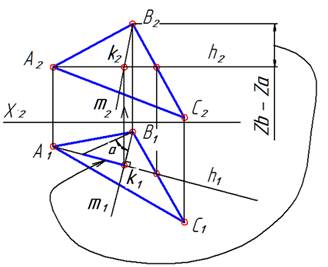
|
| Для построения угла наклона плоскости Г к плоскости проекций П2 используем фронталь. |
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 5597; Нарушение авторских прав?; Мы поможем в написании вашей работы!