
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Преобразование комплексного чертежа
|
|
|
|
| Алгоритмы, рассмотренные до настоящего момента, использовали различные вспомогательные построения, при которых исследуемые геометрические объекты оставались неподвижными, а действия выполнялись в системе неизменных плоскостей проекций, которые были заданы изначально. При изучении темы преобразование комплексного чертежа рассматривается новый подход. Здесь либо 1) геометрические объекты перемещаем в пространстве для достижения частного положения относительно существующих плоскостей проекций, либо 2) создаем новые плоскости проекций, относительно которых данные геометрические объекты будут занимать частное положение. В первом случае, когда объекты перемещаем в пространстве, применяем способы: а)вращения вокруг проецирующей прямой, б)вращения вокруг линии уровня, в)плоско-параллельного перемещения. Во втором случае, когда создаем новые плоскости проекций, применяется способ перемены (замены) плоскостей проекций. | ||
| Способ вращения вокруг проецирующей прямой. Дана прямая АВ. Требуется вращением вокруг проецирующей прямой преобразовать ее в прямую уровня. | 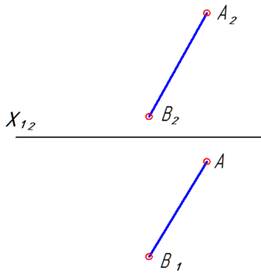
| |
| Решение. Через точку А провели горизонтально проецирующую ось i. Будем вращать прямую АВ вокруг этой оси. Тогда точка А останется неподвижной, а точка В будет совершать вращательное движение по окружности в плоскости, перпендикулярной оси вращения, то есть в горизонтальной плоскости уровня. Окружность будет проецироваться на плоскость П1 в натуральную величину. При этом, высота точки В не меняется. | 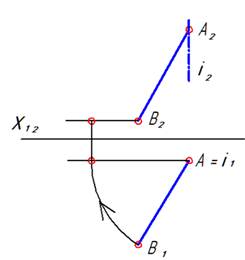
| |
| Вращение останавливаем при достижении прямой положения, параллельного плоскости проекций. В новом положении прямая становится прямой уровня (фронталью). Тогда на П2 получаем натуральную величину отрезка АВ и угол наклона к плоскости П1. На П2 можно увидеть прямоугольный треугольник, который рассматривался нами при изучении темы анализа отрезка прямой общего положения. Один катет равен горизонтальной проекции отрезка АВ. Другой катет равен разности высот концов отрезка АВ. | 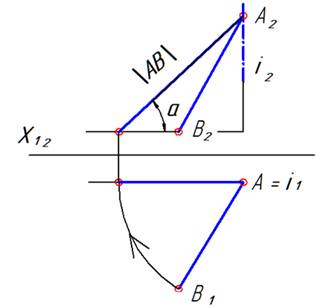
| |
| Способ перемены (замены) плоскостей проекций. | ||
| При способе замены плоскостей проекций строим новые плоскости проекций и на них проецируем геометрические объекты. Способ основывается на проецировании точки на новую плоскость проекций. Пусть в пространстве имеется точка А. | 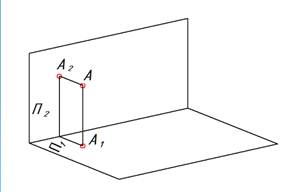
| |
| Построим новую плоскость проекций П4. Новая плоскость проекций при ортогональном проецировании должна быть перпендикулярна одной из существующих плоскостей проекций. Здесь П4 перпендикулярна плоскости П1. Положение новой плоскости проекций выбирается индивидуально в каждой задаче. | 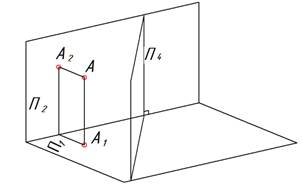
| |
| Проецируем точку А на плоскость П4. | 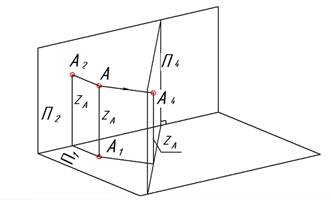
| |
| Плоскость П4 вместе с проекцией А4 поворачиваем вокруг линии пересечения плоскостей П1 и П4 (ось Х14) до совмещения с плоскостью П1. Обратим внимание на расстояние от Х14 до проекции А4. Расстояние равно высоте точки А. | 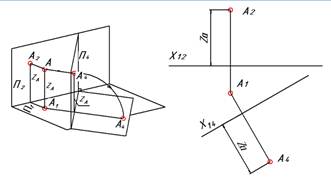
| |
| Типовые задачи, решаемый одной заменой плоскостей проекций | ||
| Задача 1. Прямую общего положения преобразовать в прямую уровня. | ||
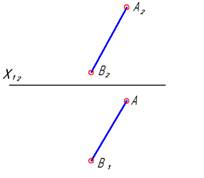
| 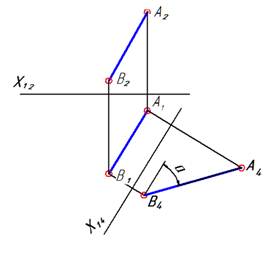 Новую плоскость проекций П4 располагаем перпендикулярно П1 и параллельно прямой АВ. На комплексном чертеже этому соответствует ось Х14, параллельная А1В1.
В новой системе плоскостей проекций П1/П4 прямая АВ стала прямой уровня, так как она параллельна П4.
Новую плоскость проекций П4 располагаем перпендикулярно П1 и параллельно прямой АВ. На комплексном чертеже этому соответствует ось Х14, параллельная А1В1.
В новой системе плоскостей проекций П1/П4 прямая АВ стала прямой уровня, так как она параллельна П4.
| |
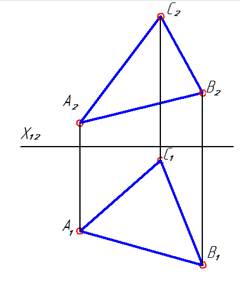
| Задача 2. Прямую уровня преобразовать в проецирующую прямую. | ||
| 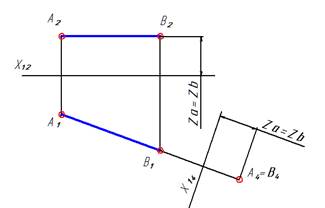 Построили плоскость П4 перпендикулярно П1 и перпендикулярно АВ. На комплексном чертеже этому соответствует положение Х14 перпендикулярно А1В1. Тогда в новой системе плоскостей проекций прямая АВ стала проецирующей прямой относительно П4.
Построили плоскость П4 перпендикулярно П1 и перпендикулярно АВ. На комплексном чертеже этому соответствует положение Х14 перпендикулярно А1В1. Тогда в новой системе плоскостей проекций прямая АВ стала проецирующей прямой относительно П4.
| |
| Задача 3. Проецирующую плоскость преобразовать в плоскость уровня. | ||
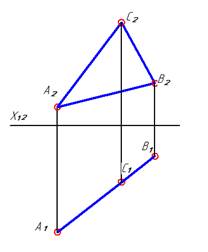
| 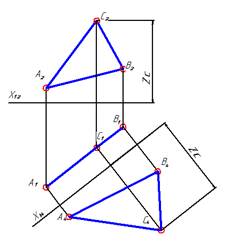 Плоскость проекций П4 построили параллельно заданной плоскости Г(АВС). На комплексном чертеже ось Х14 параллельна горизонтальному следу плоскости Г.
В новой системе плоскостей проекций П1 / П4 плоскость Г стала плоскостью уровня, как плоскость, параллельная плоскости П4.
Плоскость проекций П4 построили параллельно заданной плоскости Г(АВС). На комплексном чертеже ось Х14 параллельна горизонтальному следу плоскости Г.
В новой системе плоскостей проекций П1 / П4 плоскость Г стала плоскостью уровня, как плоскость, параллельная плоскости П4.
| |
| Задача 4. Плоскость общего положения преобразовать в проецирующую плоскость. | ||
| 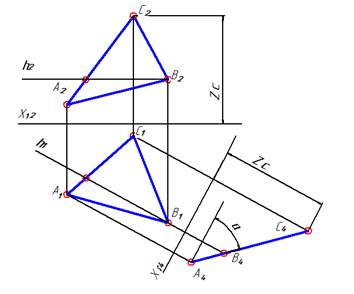 Построили плоскость П4 перпендикулярно горизонтали h плоскости Г(АВС). Тогда плоскость Г будет перпендикулярна плоскости П4, как плоскость, содержащая в себе перпендикуляр к плоскости П4.
Таким образом, в системе плоскостей проекций П1/П4 плоскость Г(АВС) стала проецирующей плоскостью. Угол a равен углу наклона плоскости Г к П1.
Построили плоскость П4 перпендикулярно горизонтали h плоскости Г(АВС). Тогда плоскость Г будет перпендикулярна плоскости П4, как плоскость, содержащая в себе перпендикуляр к плоскости П4.
Таким образом, в системе плоскостей проекций П1/П4 плоскость Г(АВС) стала проецирующей плоскостью. Угол a равен углу наклона плоскости Г к П1.
| |
| Нами рассмотрены типовые задачи, решаемые одной заменой плоскостей проекций. Задачи, решаемые двумя последовательными заменами плоскостей проекций. Задача 1. Прямую АВ общего положения преобразовать в проецирующую прямую. Алгоритм. Первая замена: применить плоскость П4, перпендикулярную П1 и параллельную прямой АВ. На комплексном чертеже ось Х14 параллельна проекции А1В1. Вторая замена: применить плоскость П5, перпендикулярную П4 и перпендикулярную прямой АВ. На комплексном чертеже ось Х45 перпендикулярна А4В4. В системе плоскостей проекций П4 / П5 прямая АВ становится проецирующей прямой, как прямая, перпендикулярная плоскости проекций П5. Задача 2. Плоскость общего положения Г преобразовать в плоскость уровня. Алгоритм. Первая замена: применить плоскость П4, перпендикулярную горизонтали h плоскости Г. На комплексном чертеже ось Х14 перпендикулярна к h1. В системе плоскостей проекций П1 / П4 плоскость Г стала проецирующей плоскостью. Плоскость Г проецируется на П4 в прямую Г4. Вторая замена: применить плоскость П5, перпендикулярную плоскости П4 и параллельную следу Г4 плоскости Г. В системе плоскостей проекций П4 / П5 плоскость Г становится плоскостью уровня. Фигуры, принадлежащие плоскости Г, проецируются на П5 в натуральную величину. | ||
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 584; Нарушение авторских прав?; Мы поможем в написании вашей работы!