Политропный процесс

Политропный процесс можно определить как термодинамический процесс изменения параметров идеального газа при постоянной теплоемкости .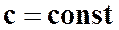

Все термодинамические процессы являются частными случаями политропного процесса.

Для политропного процесса первое начало термодинамики имеет вид

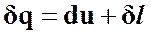(45)

или

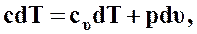(46)

где 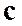¾ массовая теплоемкость газа в политропном процессе.

Также первое начало термодинамики для политропного процесса можно представить в виде

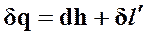(47)

или

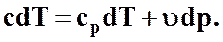(48)

Из выражения первого начала термодинамики в форме (46) найдем уравнение политропного процесса

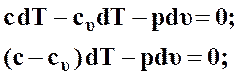(49)

Воспользуемся выражением (35)

,

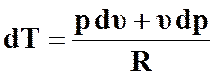тогда

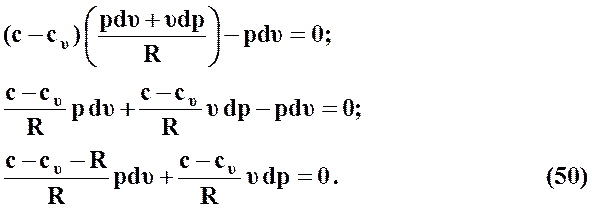
Согласно формуле Майера

,

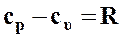тогда выражение (50) примет вид

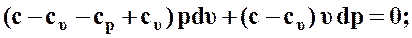
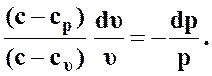(51)

Обозначим отношение

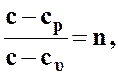
где 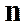¾ показатель политропы.

Тогда

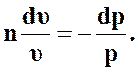(52)

Проинтегрируем выражение (52)

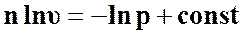(53)

или

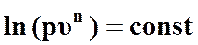. (54)

Таким образом, если логарифм некоторой функции величина постоянная, то и сама функция является постоянной величиной

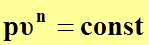. (55)

Выражение (55) представляет собой уравнение политропного процесса.

Выразим теплоемкость идеального газа в политропном процессе через известную изохорную теплоемкость.

Из выражения для показателя политропы

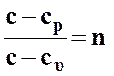и показателя адиабаты 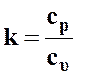имеем

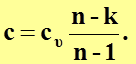(56)

С учетом выражения (46) и уравнения состояния 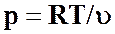можно записать

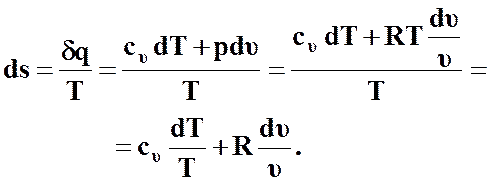(57)

В интегральной форме первое начало термодинамики для политропного процесса будет иметь вид

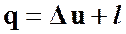(58)

или

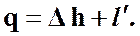(59)

Из выражений (45) ─ (59) следует, что для политропного процесса идеального газа :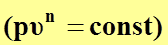

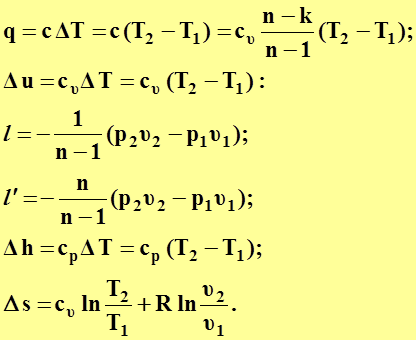(60)

Показать политропы 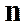может меняться от 0 до µ.

Рассмотрим частные случаи:

1. при 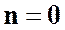уравнение политропного процесса 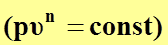переходит в уравнение изобарного процесса ;

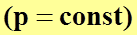2. при 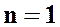уравнение политропного процесса 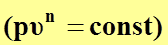переходит в уравнение изотермического процесса ;

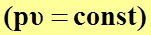3. при 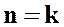уравнение политропного процесса 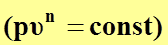переходит в уравнение адиабатного процесса .

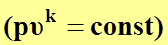4. при 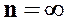уравнение политропного процесса 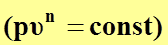переходит в уравнение изохорного процесса .

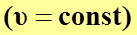На рисунках 5 и 6 изображены все представленные термодинамические процессы в 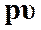и 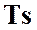─ диаграммах.

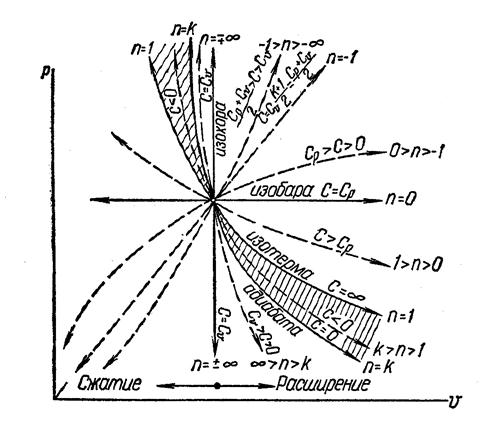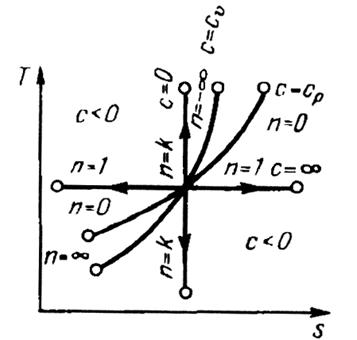Рис. 5 Изображение основных процессов в 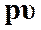- диаграмме

Рис. 6. Изображение основных термодинамических процессов

в 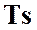- диаграмме

Все процессы начинаются в одной точке (в центре).

Изохора 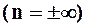делит поле диаграммы на две области: процессы, находящиеся правее изохоры, характеризуются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных левее изохоры, характерна отрицательная работа.

Процессы, расположенные правее и выше адиабаты, идут с подводом теплоты к рабочему телу; процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты.

Для процессов, расположенных над изотермой 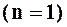, характерно увеличение внутренней энергии газа; процессы, расположенные под изотермой, сопровождаются уменьшением внутренней энергии.

Процессы, расположенные между адиабатой и изотермой, имеют отрицательную теплоемкость, так как 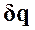и 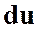(а, следовательно, и 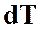), имеют в этой области противоположные знаки. В таких процессах 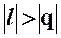, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.

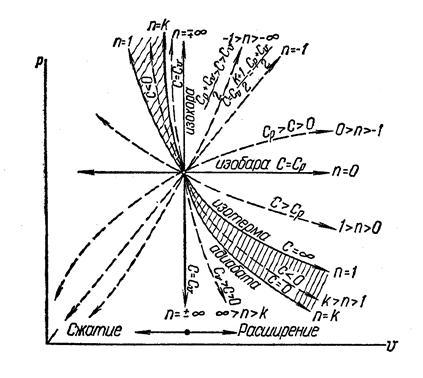
Рис. 5 Изображение основных процессов в - диаграмме

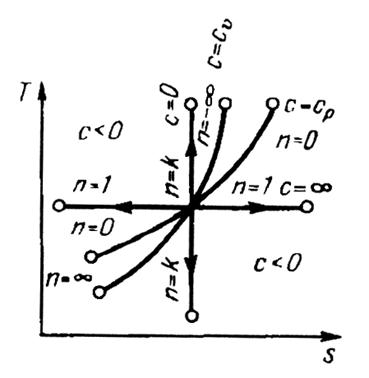Рис. 6. Изображение основных термодинамических процессов в - диаграмме

Дата добавления: 2014-01-03